【題目】2018年9月17日世界人工智能大會在．上海召開，人工智能的變革力在教育、制造等領域加速落地．在某市舉辦的一次中學生機器人足球賽中，有四個代表隊進入決賽，決賽中，每個隊分別與其它三個隊進行主客場比賽各一場(即每個隊要進行6場比賽)，以下是積分表的一-部分．
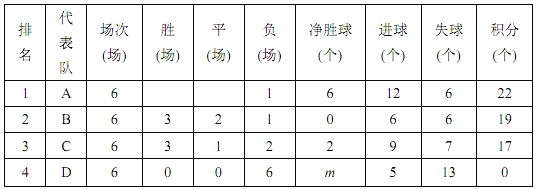
(說明：積分=勝場積分十平場積分+負場積分)
（1）D代表隊的凈勝球數m=______；
（2）本次決賽中，勝一場積______分，平一場積______分，負一場積_______分；
（3）此次競賽的獎金分配方案為：進入決賽的每支代表隊都可以獲得參賽獎金6000元；另外，在決賽期間，每勝一場可以再獲得獎金2000元，每平一場再獲得獎金1000元．請根據表格提供的信息，求出冠軍A隊一共能獲得多少獎金．
每日10分鐘口算心算速算天天練系列答案科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，直線y＝x＋b與雙曲線y＝
的一個交點為A(2，4)，與y軸交于點B.
(1)求m的值和點B的坐標；
(2)點P在雙曲線y＝
上，△OBP的面積為8，直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某數學“綜合與實踐”小組的同學把“測量斜拉索頂端到橋面的距離”作為一項課題活動，他們制訂了測量方案，并利用課余時間借助該橋斜拉索完成了實地測量．測量結果如下：如圖，兩側最長斜拉索
，
相交于點
，分別與橋面交于
，
兩點，且點，，在同一豎直平面內．測得
，
，
米，請幫助該小組根據測量數據，求斜拉索頂端點到
的距離．（參考數據：
，
，
，
，
，
．）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某旅行社的一則廣告如下：
甲公司想分批組織員工到延安紅色旅游學習．
（1）如果第一批組織40人去學習，則公司應向旅行社交費 元；
（2）如果公司計劃用29250元組織第一批員工去學習，問這次旅游學習應安排多少人參加？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸、
軸分別相交于
、
兩點，拋物線
經過點，交軸正半軸于點
．
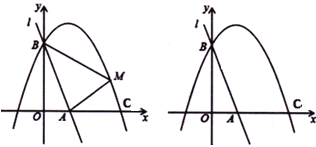
（1）求該拋物線的函數表達式；
（2）已知點
是拋物線上的一個動點，并且點在第一象限內，連接
、
，設點的橫坐標為
，
的面積為
，求與的函數表達式，并求出的最大值及此時動點的坐標；
（3）將點繞原點旋轉得點
，連接
、
，在旋轉過程中，一動點
從點出發，沿線段以每秒
個單位的速度運動到，再沿線段
以每秒
個單位長度的速度運動到后停止，求點在整個運動過程中用時最少是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，對于任意兩點P1(x1，y1)，P2(x2，y2)，如果
，則稱P1與P2互為“d-距點”．例如：點P1(3，6)，點P2(1，7)，由d=|3-1|+|6-7|=3，可得點P1與P2互為“3-距點”．
（1）在點D(-2，-2)，E(5，-1)，F(0，4)中，原點O的“4-距點"是____(填字母)；
（2）已知點A(2，1)，點B(0，b)，過點B作平行于x軸的直線l．
①當b=3時，直線l上點A的“2-距點"的坐標為_______；
②若直線l上存在點A的2-距點”，求b的取值范圍：
（3）已知點M(1，2)，N(3，2)，C(m，0)，⊙C的半徑為
，若在線段MN上存在點P，在⊙C上存在點Q，使得點P與點Q互為“5-距點"，直接寫出m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解七年級學生身體發育狀況，學校抽取一部分學生測量身高（單位：m），繪制處如下的統計圖①和圖②．請根據相關信息，解答下列問題：
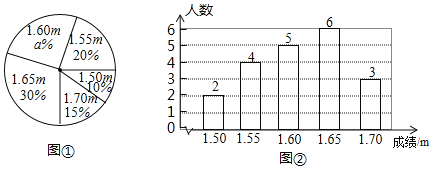
（1）圖①中a的值為 ；
（2）求統計的這組學生身高數據的平均數、眾數和中位數；
（3）如果全校七年級學生有300人，那么估計身高大于1.65m的學生大約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對垃圾進行分類投放，能提高垃圾處理和再利用的效率，減少污染，保護環境．為了檢查垃圾分類的落實情況，某居委會成立了甲、乙兩個檢查組，采取隨機抽查的方式分別對轄區內的A，B，C，D四個小區進行檢查，并且每個小區不重復檢查．
（1）甲組抽到A小區的概率是多少；
（2）請用列表或畫樹狀圖的方法求甲組抽到A小區，同時乙組抽到C小區的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC 中，AB=AC，點 M 在 BA 的延長線上，點 N 在 BC 的延長線上，過點 C 作CD∥AB 交∠CAM 的平分線于點 D．
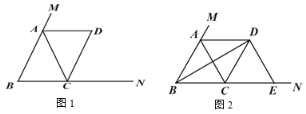
（1）如圖 1，求證：四邊形 ABCD 是平行四邊形；
（2）如圖 2，當∠ABC=60°時，連接 BD，過點 D 作 DE⊥BD，交 BN 于點 E，在不添加任何輔助線的情況下，請直接寫出圖 2 中四個三角形（不包含△CDE），使寫出的每個三角形的面積與△CDE 的面積相等．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
