
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)P是直線(xiàn)
,點(diǎn)P是直線(xiàn)![]() 上一點(diǎn),且
上一點(diǎn),且![]() ,則點(diǎn)P的坐標(biāo)為______.
,則點(diǎn)P的坐標(biāo)為______.

【答案】![]()
【解析】
由于題目中給出![]() ,則可考慮構(gòu)造等腰直角三角形進(jìn)行解決,將AB順時(shí)針旋轉(zhuǎn)
,則可考慮構(gòu)造等腰直角三角形進(jìn)行解決,將AB順時(shí)針旋轉(zhuǎn)![]() 得到線(xiàn)段BC,求出點(diǎn)C的坐標(biāo),連接AC,則AC與BP的交點(diǎn)M即為線(xiàn)段AC的中點(diǎn),可求出M的坐標(biāo),則直線(xiàn)BP的解析式亦可求的,再將直線(xiàn)
得到線(xiàn)段BC,求出點(diǎn)C的坐標(biāo),連接AC,則AC與BP的交點(diǎn)M即為線(xiàn)段AC的中點(diǎn),可求出M的坐標(biāo),則直線(xiàn)BP的解析式亦可求的,再將直線(xiàn)![]() 與直線(xiàn)BP的解析式聯(lián)立成方程組,即可求出點(diǎn)P的坐標(biāo).
與直線(xiàn)BP的解析式聯(lián)立成方程組,即可求出點(diǎn)P的坐標(biāo).
如圖所示,

將線(xiàn)段AB繞點(diǎn)B順時(shí)針旋轉(zhuǎn)![]() 得到線(xiàn)段BC,則點(diǎn)C的坐標(biāo)為
得到線(xiàn)段BC,則點(diǎn)C的坐標(biāo)為![]() ,
,
由于旋轉(zhuǎn)可知,![]() 為等腰直角三角形,令線(xiàn)段AC和線(xiàn)段BP交于點(diǎn)M,則M為線(xiàn)段AC的中點(diǎn),
為等腰直角三角形,令線(xiàn)段AC和線(xiàn)段BP交于點(diǎn)M,則M為線(xiàn)段AC的中點(diǎn),
所以點(diǎn)M的坐標(biāo)為![]() ,又B為
,又B為![]() ,設(shè)直線(xiàn)BP為
,設(shè)直線(xiàn)BP為![]() ,將點(diǎn)B和點(diǎn)M代入可得
,將點(diǎn)B和點(diǎn)M代入可得![]() ,
,
解得![]() ,
,![]() ,可得直線(xiàn)BP為
,可得直線(xiàn)BP為![]() ,由于點(diǎn)P為直線(xiàn)BP和直線(xiàn)
,由于點(diǎn)P為直線(xiàn)BP和直線(xiàn)![]() 的交點(diǎn),
的交點(diǎn),
則由![]() 解得
解得![]() ,所以點(diǎn)P的坐標(biāo)為
,所以點(diǎn)P的坐標(biāo)為![]() ,
,
故答案為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】清朝康熙皇帝是我國(guó)歷史上對(duì)數(shù)學(xué)很有興趣的帝王近日,西安發(fā)現(xiàn)了他的數(shù)學(xué)專(zhuān)著,其中有一文《積求勾股法》,它對(duì)“三邊長(zhǎng)為3、4、5的整數(shù)倍的直角三角形,已知面積求邊長(zhǎng)”這一問(wèn)題提出了解法:“若所設(shè)者為積數(shù)(面積),以積率六除之,平方開(kāi)之得數(shù),再以勾股弦各率乘之,即得勾股弦之?dāng)?shù)”.用現(xiàn)在的數(shù)學(xué)語(yǔ)言表述是:“若直角三角形的三邊長(zhǎng)分別為3、4、5的整數(shù)倍,設(shè)其面積為S,則第一步: ![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分別用3、4、5乘以k,得三邊長(zhǎng)”.
=k;第三步:分別用3、4、5乘以k,得三邊長(zhǎng)”.
(1)當(dāng)面積S等于150時(shí),請(qǐng)用康熙的“積求勾股法”求出這個(gè)直角三角形的三邊長(zhǎng);
(2)你能證明“積求勾股法”的正確性嗎?請(qǐng)寫(xiě)出證明過(guò)程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,將矩形ABCD沿AF折疊,使點(diǎn)D落在BC邊的點(diǎn)E處,過(guò)點(diǎn)E作EG∥CD交AF于點(diǎn)G,連接DG.
(1)求證:四邊形EFDG是菱形;
(2)求證:EG2= ![]() AFGF;
AFGF;
(3)若AG=6,EG=2 ![]() ,求BE的長(zhǎng).
,求BE的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地的一座人行天橋如圖所示,天橋高為6米,坡面BC的坡度為1:1,為了方便行人推車(chē)過(guò)天橋,有關(guān)部門(mén)決定降低坡度,使新坡面的坡度為1: ![]() .
.
(1)求新坡面的坡角a;
(2)原天橋底部正前方8米處(PB的長(zhǎng))的文化墻PM是否需要拆除?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一次藝術(shù)作品制作比賽中,某小組八件作品的成績(jī)![]() 單位:分
單位:分![]() 分別是:7、9、8、9、8、10、9、7,下列說(shuō)法不正確的是
分別是:7、9、8、9、8、10、9、7,下列說(shuō)法不正確的是![]()
![]()
A. 中位數(shù)是![]() B. 平均數(shù)是
B. 平均數(shù)是![]() C. 眾數(shù)是9D. 極差是3
C. 眾數(shù)是9D. 極差是3
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中:①0是最小的整數(shù);②有理數(shù)不是正數(shù)就是負(fù)數(shù);③非負(fù)數(shù)就是正數(shù);④![]() 不僅是有理數(shù),而且是分?jǐn)?shù);⑤
不僅是有理數(shù),而且是分?jǐn)?shù);⑤![]() 是無(wú)限不循環(huán)小數(shù),所以不是有理數(shù);⑥無(wú)限小數(shù)不都是有理數(shù);⑦正數(shù)中沒(méi)有最小的數(shù),負(fù)數(shù)中沒(méi)有最大的數(shù).其中錯(cuò)誤的說(shuō)法的個(gè)數(shù)為( )
是無(wú)限不循環(huán)小數(shù),所以不是有理數(shù);⑥無(wú)限小數(shù)不都是有理數(shù);⑦正數(shù)中沒(méi)有最小的數(shù),負(fù)數(shù)中沒(méi)有最大的數(shù).其中錯(cuò)誤的說(shuō)法的個(gè)數(shù)為( )
A.7個(gè)B.6個(gè)C.5個(gè)D.4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某電視臺(tái)“走基層”欄目的一位記者乘汽車(chē)赴360km外的農(nóng)村采訪(fǎng),全程的前一部分為高速公路,后一部分為鄉(xiāng)村公路.若汽車(chē)在高速公路和鄉(xiāng)村公路上分別以某一速度勻速行駛,汽車(chē)行駛的路程y(單位:km)與時(shí)間x(單位:h)之間的關(guān)系如圖所示,則下列結(jié)論正確的是【 】

(A)汽車(chē)在高速公路上的行駛速度為100km/h
(B)鄉(xiāng)村公路總長(zhǎng)為90km
(C)汽車(chē)在鄉(xiāng)村公路上的行駛速度為60km/h
(D)該記者在出發(fā)后4.5h到達(dá)采訪(fǎng)地
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
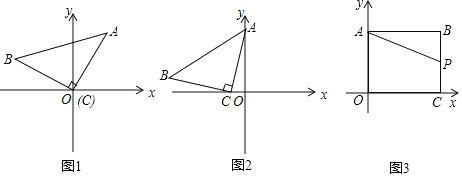
【題目】![]() 操作思考:如圖1,在平面直角坐標(biāo)系中,等腰
操作思考:如圖1,在平面直角坐標(biāo)系中,等腰![]() 的直角頂點(diǎn)C在原點(diǎn),將其繞著點(diǎn)O旋轉(zhuǎn),若頂點(diǎn)A恰好落在點(diǎn)
的直角頂點(diǎn)C在原點(diǎn),將其繞著點(diǎn)O旋轉(zhuǎn),若頂點(diǎn)A恰好落在點(diǎn)![]() 處
處![]() 則
則![]() 的長(zhǎng)為______;
的長(zhǎng)為______;![]() 點(diǎn)B的坐標(biāo)為______
點(diǎn)B的坐標(biāo)為______![]() 直接寫(xiě)結(jié)果
直接寫(xiě)結(jié)果![]()
![]() 感悟應(yīng)用:如圖2,在平面直角坐標(biāo)系中,將等腰
感悟應(yīng)用:如圖2,在平面直角坐標(biāo)系中,將等腰![]() 如圖放置,直角頂點(diǎn)
如圖放置,直角頂點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,試求直線(xiàn)AB的函數(shù)表達(dá)式.
,試求直線(xiàn)AB的函數(shù)表達(dá)式.
![]() 拓展研究:如圖3,在直角坐標(biāo)系中,點(diǎn)
拓展研究:如圖3,在直角坐標(biāo)系中,點(diǎn)![]() ,過(guò)點(diǎn)B作
,過(guò)點(diǎn)B作![]() 軸,垂足為點(diǎn)A,作
軸,垂足為點(diǎn)A,作![]() 軸,垂足為點(diǎn)C,P是線(xiàn)段BC上的一個(gè)動(dòng)點(diǎn),點(diǎn)Q是直線(xiàn)
軸,垂足為點(diǎn)C,P是線(xiàn)段BC上的一個(gè)動(dòng)點(diǎn),點(diǎn)Q是直線(xiàn)![]() 上一動(dòng)點(diǎn)
上一動(dòng)點(diǎn)![]() 問(wèn)是否存在以點(diǎn)P為直角頂點(diǎn)的等腰
問(wèn)是否存在以點(diǎn)P為直角頂點(diǎn)的等腰![]() ,若存在,請(qǐng)求出此時(shí)P的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
,若存在,請(qǐng)求出此時(shí)P的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在大樓AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小紅在斜坡下的點(diǎn)C處測(cè)得樓頂B的仰角為60°,在斜坡上的點(diǎn)D處測(cè)得樓頂B的仰角為45°,其中點(diǎn)A,C,E在同一直線(xiàn)上.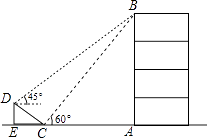
(1)求斜坡CD的高度DE;
(2)求大樓AB的高度(結(jié)果保留根號(hào))
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com