
【題目】操作:“如圖1,P是平面直角坐標系中一點(x軸上的點除外),過點P作PC⊥x軸于點C,點C繞點P逆時針旋轉60°得到點Q.”我們將此由點P得到點Q的操作稱為點的T變換.
(1)點P(a,b)經過T變換后得到的點Q的坐標為 ![]() ;若點M經過T變換后得到點N(6,﹣
;若點M經過T變換后得到點N(6,﹣ ![]() ),則點M的坐標為
),則點M的坐標為 ![]() .
.
(2)A是函數y= ![]() x圖象上異于原點O的任意一點,經過T變換后得到點B.
x圖象上異于原點O的任意一點,經過T變換后得到點B.
①求經過點O,點B的直線的函數表達式;
②如圖2,直線AB交y軸于點D,求△OAB的面積與△OAD的面積之比.
【答案】
(1)
如圖1,連接CQ,過Q作QD⊥PC于點D,
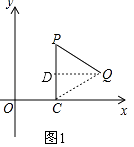
由旋轉的性質可得PC=PQ,且∠CPQ=60°,
∴△PCQ為等邊三角形,
∵P(a,b),
∴OC=a,PC=b,
∴CD= ![]() PC=
PC= ![]() b,DQ=
b,DQ= ![]() PQ=
PQ= ![]() b,
b,
∴Q(a+ ![]() b,
b, ![]() b);
b);
設M(x,y),則N點坐標為(x+ ![]() y,
y, ![]() y),
y),
∵N(6,﹣ ![]() ),
),
∴ 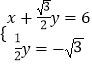 ,解得
,解得 ![]() ,
,
∴M(9,﹣2 ![]() );
);
故答案為:(a+ ![]() b,
b, ![]() b);(9,﹣2
b);(9,﹣2 ![]() )
)
(2)
①∵A是函數y= ![]() x圖象上異于原點O的任意一點,
x圖象上異于原點O的任意一點,
∴可取A(2, ![]() ),
),
∴2+ ![]() ×
× ![]() =
= ![]() ,
, ![]() ×
× ![]() =
= ![]() ,
,
∴B( ![]() ,
, ![]() ),
),
設直線OB的函數表達式為y=kx,則 ![]() k=
k= ![]() ,解得k=
,解得k= ![]() ,
,
∴直線OB的函數表達式為y= ![]() x;
x;
②設直線AB解析式為y=k′x+b,
把A、B坐標代入可得 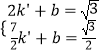 ,解得
,解得 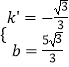 ,
,
∴直線AB解析式為y=﹣ ![]() x+
x+ ![]() ,
,
∴D(0, ![]() ),且A(2,
),且A(2, ![]() ),B(
),B( ![]() ,
, ![]() ),
),
∴AB= ![]() =
= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(1)連接CQ可知△PCQ為等邊三角形,過Q作QD⊥PC,利用等邊三角形的性質可求得CD和QD的長,則可求得Q點坐標;設出M點的坐標,利用P、Q坐標之間的關系可得到點M的方程,可求得M點的坐標;(2)①可取A(2, ![]() ),利用T變換可求得B點坐標,利用待定系數示可求得直線OB的函數表達式;②由待定系數示可求得直線AB的解析式,可求得D點坐標,則可求得AB、AD的長,可求得△OAB的面積與△OAD的面積之比.
),利用T變換可求得B點坐標,利用待定系數示可求得直線OB的函數表達式;②由待定系數示可求得直線AB的解析式,可求得D點坐標,則可求得AB、AD的長,可求得△OAB的面積與△OAD的面積之比.
【考點精析】本題主要考查了一次函數的性質和一次函數的圖象和性質的相關知識點,需要掌握一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠才能正確解答此題.


科目:初中數學 來源: 題型:
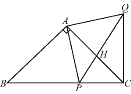
【題目】如圖,在△ABC中,AB=AC,∠BAC=90°,點P是BC上的一動點,AP=AQ,∠PAQ=90°,連接CQ.
(1)求證:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,請直接寫出此時點P的位置;若不能,請說明理由.
(3)當點P在BC上什么位置時,△ACQ是等腰三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“表1”為初三(1)班全部43名同學某次數學測驗成績的統計結果,則下列說法正確的是( )
成績(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成績大于女生的平均成績
B.男生的平均成績小于女生的平均成績
C.男生成績的中位數大于女生成績的中位數
D.男生成績的中位數小于女生成績的中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,我們把,每個小正方形的頂點叫做格點,連接任意兩個格點的線段叫網格線段,以網格線段為邊組成的圖形叫做格點圖形,在下列如圖所示的正方形網格中,每個小正方形的邊長為1. 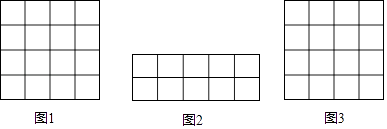
(1)請你在圖1中畫一個格點圖形,且該圖形是邊長為 ![]() 的菱形;
的菱形;
(2)請你在圖2中用網格線段將其切割成若干個三角形和正方形,拼接成一個與其面積相等的正方形,并在圖3中畫出格點正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.
《九章算術》中記載:“今有牛五、羊二,直金十兩;牛二、羊五,直金八兩.問:牛、羊各直金幾何?”
譯文:“假設有5頭牛、2只羊,值金10兩;2頭牛、5只羊,值金8兩.問:每頭牛、每只羊各值金多少兩?”
設每頭牛值金x兩,每只羊值金y兩,可列方程組為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景
在數學活動課上,張老師要求同學們拿兩張大小不同的矩形紙片進行旋轉變換探究活動.如圖1,在矩形紙片ABCD和矩形紙片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,點E是AD的中點,矩形紙片EFGH以點E為旋轉中心進行逆時針旋轉,在旋轉過程中會產生怎樣的數量關系,提出恰當的數學問題并加以解決.
解決問題
下面是三個學習小組提出的數學問題,請你解決這些問題.
(1)“奮進”小組提出的問題是:如圖1,當EF與AB相交于點M,EH與BC相交于點N時,求證:EM=EN.
(2)“雄鷹”小組提出的問題是:在(1)的條件下,當AM=CN時,AM與BM有怎樣的數量關系,說明理由.
(3)“創新”小組提出的問題是;若矩形EFGH繼續以點E為旋轉中心進行逆時針旋轉,當∠AEF=60°時,請你在圖2中畫出旋轉后的示意圖,并求出此時EF將邊BC分成的兩條線段的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:如果10b=n,那么稱b為n的勞格數,記為b= d(n).
(1)根據勞格數的定義,可知d(10)=1,d(102)=2,直接寫出 d(103)的值.
(2)勞格數有如下運算性質:若m,n為正數,則d(mn)= d(m)+ d(n);d(![]() )= d(m)- d(n).
)= d(m)- d(n).
根據運算性質,求:![]() ,若
,若 ![]() ,直接寫出
,直接寫出![]() ,
,![]() 的值.
的值.
(3)下表中與數x對應的勞格數 ![]() 有且只有兩個是錯誤的,請找出錯誤的勞格數并改正.
有且只有兩個是錯誤的,請找出錯誤的勞格數并改正.
| 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com