
【題目】如圖,在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 分別交x軸、y軸于A,B兩點,經(jīng)過A,B兩點的拋物線
分別交x軸、y軸于A,B兩點,經(jīng)過A,B兩點的拋物線![]() 與x軸的正半軸相交于點
與x軸的正半軸相交于點![]() .
.

(1)求拋物線的解析式;
(2)若P為線段AB上一點,![]() ,求AP的長;
,求AP的長;
(3)在(2)的條件下,設(shè)M是y軸上一點,試問:拋物線上是否存在點N,使得以A,P,M,N為頂點的四邊形為平行四邊形?若存在,求出點N的坐標(biāo);若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,點N的坐標(biāo)為(
;(3)存在,點N的坐標(biāo)為(![]() ,3) 或(
,3) 或(![]() ,
,![]() )
)
【解析】
(1)利用直線![]() 與y軸的交點求得點B的坐標(biāo),然后把點B、C的坐標(biāo)代入
與y軸的交點求得點B的坐標(biāo),然后把點B、C的坐標(biāo)代入![]() ,即可求解;
,即可求解;
(2)先求得點A的坐標(biāo),證得△PAO![]() △CAB,利用對應(yīng)邊成比例即可求解;
△CAB,利用對應(yīng)邊成比例即可求解;
(3)分點N在AB的上方或下方兩種情況進行討論,根據(jù)平行四邊形的性質(zhì)和等腰直角三角形的性質(zhì),利用三角形全等,即可求解.
(1)令![]() ,則
,則![]() ,
,
∴點B的坐標(biāo)為(0,3),
拋物線![]() 經(jīng)過點B (0,3),C (1,0),
經(jīng)過點B (0,3),C (1,0),
∴![]() ,解得
,解得![]() ,
,
∴拋物線的解析式為:![]() ;
;
(2)令![]() ,則
,則![]() ,
,
解得:![]() ,
,
∴點A的坐標(biāo)為(![]() ,0),
,0),
∴OA=3,OB=3,OC=1,
![]() ,
,
∵![]() ,且
,且![]() ,
,
∴△PAO![]() △CAB,
△CAB,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
(3)存在,
過點P作PD⊥x軸于點D,
∵OA=3,OB=3,∠AOB=![]() ,
,
∴∠BAO=∠ABO=![]() ,
,
∴△PAD為等腰直角三角形,
∵![]() ,
,
∴PD=AD=2,
∴點P的坐標(biāo)為(![]() ,2),
,2),
當(dāng)N在AB的上方時,過點N作NE⊥y軸于點E,如圖,
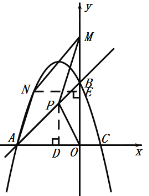
∵四邊形APMN為平行四邊形,
∴NM∥AP,NM=AP=![]() ,
,
∴∠NME=∠ABO=![]() ,
,
∴△NME為等腰直角三角形,
∴Rt△NME![]() Rt△APD,
Rt△APD,
∴NE=AD=2,
當(dāng)![]() 時,
時,![]() ,
,
∴點N的坐標(biāo)為(![]() ,3),
,3),
當(dāng)N在AB的下方時,過點N作NF⊥y軸于點F,如圖,
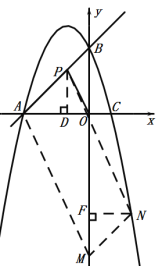
同理可得:Rt△NMF![]() Rt△APD,
Rt△APD,
∴NF=AD=2,
當(dāng)![]() 時,
時,![]() ,
,
∴點N的坐標(biāo)為(![]() ,
,![]() ),
),
綜上,點N的坐標(biāo)為(![]() ,3) 或(
,3) 或(![]() ,
,![]() ) .
) .


科目:初中數(shù)學(xué) 來源: 題型:
【題目】合理飲食對學(xué)生的身體、智力發(fā)育和健康起到了極其重要的作用,只有葷食和素食的合理搭配,才能強化初中生的身體素質(zhì),某校為了解學(xué)生的體質(zhì)健康狀況,以便食堂為學(xué)生提供合理膳食,對本校七年級、八年級學(xué)生的體質(zhì)健康狀況進行了調(diào)查,過程如下:
收集數(shù)據(jù):
從七、八年級兩個年級中各抽取![]() 名學(xué)生,進行了體質(zhì)健康測試,測試成績(百分制)如下:
名學(xué)生,進行了體質(zhì)健康測試,測試成績(百分制)如下:
七年級:![]()
八年級:![]()
整理數(shù)據(jù):
年級 |
|
|
|
|
七年級 |
|
|
|
|
八年級 |
|
|
|
|
(說明:![]() 為優(yōu)秀,
為優(yōu)秀,![]() 為良好,
為良好,![]() 為及格,
為及格,![]() 為不及格)
為不及格)
分析數(shù)據(jù):
年級 | 平均數(shù) | 中位數(shù) | 眾數(shù) |
七年級 |
|
|
|
八年級 |
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ,
,
(2)比較這兩組樣本數(shù)據(jù)的平均數(shù)、中位數(shù)和眾數(shù),你認(rèn)為哪個年級的體質(zhì)健康成績比較好?請說明理由
(3)若七年級共有![]() 名學(xué)生,請估計七年級體質(zhì)健康成績優(yōu)秀的學(xué)生人數(shù)
名學(xué)生,請估計七年級體質(zhì)健康成績優(yōu)秀的學(xué)生人數(shù)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,AB=2,動點E從點A出發(fā)向點D運動,同時動點F從點D出發(fā)向點C運動,點E、F運動的速度相同,當(dāng)它們到達各自終點時停止運動,運動過程中線段AF、BE相交于點P,M是線段BC上任意一點,則MD+MP的最小值為 .
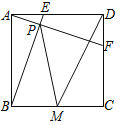
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為斜邊
為斜邊![]() 的中線,過點D作
的中線,過點D作![]() 于點E,延長
于點E,延長![]() 至點F,使
至點F,使![]() ,連接
,連接![]() ,點G在線段
,點G在線段![]() 上,連接
上,連接![]() ,且
,且![]() .下列結(jié)論:①
.下列結(jié)論:①![]() ;②四邊形
;②四邊形![]() 是平行四邊形;③
是平行四邊形;③![]() ;④
;④![]() .其中正確結(jié)論的個數(shù)是( )
.其中正確結(jié)論的個數(shù)是( )
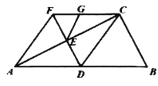
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解同學(xué)們最喜歡一年四季中的哪個季節(jié),數(shù)學(xué)社在全校隨機抽取部分同學(xué)進行問卷調(diào)查,根據(jù)調(diào)查結(jié)果,得到如下兩幅不完整的統(tǒng)計圖.

根據(jù)圖中信息,解答下列問題:
(1)此次調(diào)查一共隨機抽取了________名同學(xué);扇形統(tǒng)計圖中,“春季”所對應(yīng)的扇形的圓心角的度數(shù)為________;
(2)若該學(xué)校有1500名同學(xué),請估計該校最喜歡冬季的同學(xué)的人數(shù);
(3)現(xiàn)從最喜歡夏季的3名同學(xué)A,B,C中,隨機選兩名同學(xué)去參加學(xué)校組織的“我愛夏天”演講比賽,請用列表或畫樹狀圖的方法求恰好選到A,B去參加比賽的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】[問題解答]
兩個城鎮(zhèn)![]() 與一條公路
與一條公路![]() 位置如圖①所示.現(xiàn)電信部門需在公路
位置如圖①所示.現(xiàn)電信部門需在公路![]() 上修建一座信號發(fā)射塔
上修建一座信號發(fā)射塔![]() 要求發(fā)射塔
要求發(fā)射塔![]() 到兩個城鎮(zhèn)
到兩個城鎮(zhèn)![]() 與
與![]() 的距離之和最短.
的距離之和最短.
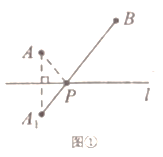
解:點![]() 作關(guān)于直線
作關(guān)于直線![]() 的對稱點
的對稱點![]() 連結(jié)
連結(jié)![]() ,
,
與直線![]() 的交點即為所求的點
的交點即為所求的點![]() .
.
![]() 點
點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,
對稱,
![]() 直線
直線![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 點
點![]() 即為所求的點。(兩點之間線段最短)
即為所求的點。(兩點之間線段最短)
請根據(jù)以上問題解答,完成下列問題.
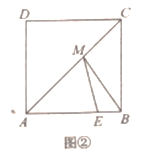
[方法運用]如圖②,在正方形![]() 中,
中,![]() 點
點![]() 在邊
在邊![]() 上,點
上,點![]() 在對角線AC上,
在對角線AC上,
(1)當(dāng)點![]() 是邊
是邊![]() 的中點時,則
的中點時,則![]() 的最小值為 ;
的最小值為 ;
(2)若![]() 求
求![]() 周長的最小值.
周長的最小值.
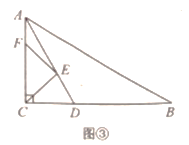
[拓展提升]如圖③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于點
于點![]() ,點
,點![]() 分別在
分別在![]() 上,則
上,則![]() 的最小值為 .
的最小值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
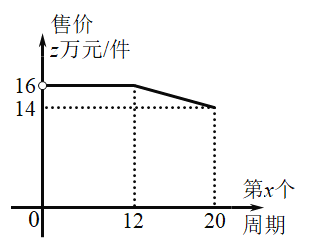
【題目】某工廠計劃在每個生產(chǎn)周期內(nèi)生產(chǎn)并銷售完某型設(shè)備,設(shè)備的生產(chǎn)成本為10萬元/件(1)如圖,設(shè)第x(0<x≤20)個生產(chǎn)周期設(shè)備售價z萬元/件,z與x之間的關(guān)系用圖中的函數(shù)圖象表示,求z關(guān)于x的函數(shù)解析式(寫出x的范圍).
(2)設(shè)第x個生產(chǎn)周期生產(chǎn)并銷售的設(shè)備為y件,y與x滿足關(guān)系式y=5x+40(0<x≤20).在(1)的條件下,工廠在第幾個生產(chǎn)周期創(chuàng)造的利潤最大?最大為多少萬元?(利潤=收入-成本)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,拋物線![]() 與兩條坐標(biāo)軸分別交于
與兩條坐標(biāo)軸分別交于![]() ,
,![]() ,
,![]() 三點.其中
三點.其中![]() ,且
,且![]() .
.
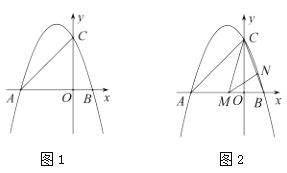
(1)求該拋物線的解析式;
(2)點![]() 是
是![]() 軸上一點,拋物線上是否存在點
軸上一點,拋物線上是否存在點![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點,以
為頂點,以![]() 為邊的四邊形是平行四邊形?若存在,求出點
為邊的四邊形是平行四邊形?若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由;
的坐標(biāo);若不存在,請說明理由;
(3)如圖2,點![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 上的動點,連接
上的動點,連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時,求點
時,求點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是
是![]() 的外接圓,AD為
的外接圓,AD為![]() 的直徑,
的直徑,![]() ,垂足為E,連接BO,延長BO交AC于點F.
,垂足為E,連接BO,延長BO交AC于點F.
(1)如圖1,求證:![]() ;
;
(2)如圖2,過點D作![]() ,交
,交![]() 于點G,點H為GD的中點,連接OH,求證:
于點G,點H為GD的中點,連接OH,求證:![]() ;
;
(3)如圖3,在(2)的條件下,連接CG,若![]() 的面積為
的面積為![]() ,求線段CG的長.
,求線段CG的長.
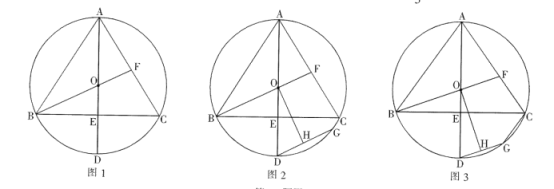
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com