
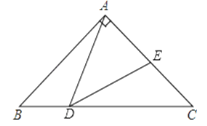
【題目】如圖所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,點D在BC上運動(不能到達點B,C),過點D作∠ADE=45°,DE交AC于點E.
(1)求證:△ABD∽△DCE;
(2)當△ADE是等腰三角形時,求AE的長.
【答案】(1)見解析;(2)1
【解析】
(1)首先根據(jù)等腰直角三角形的兩個底角都是45![]() ,得到一對對應角相等;再根據(jù)三角形的外角的性質(zhì)得到∠ADE+∠EDC=∠B+∠BAD,從而證明∠EDC=∠BAD,根據(jù)兩個角對應相等,得到兩個三角形相似;
,得到一對對應角相等;再根據(jù)三角形的外角的性質(zhì)得到∠ADE+∠EDC=∠B+∠BAD,從而證明∠EDC=∠BAD,根據(jù)兩個角對應相等,得到兩個三角形相似;
(2)根據(jù)等腰三角形的定義,此題要分AD=AE、AD=DE、AE=DE三種情況進行分析討論.
(1)證明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:討論:①若AD=AE時,∠DAE=90°,此時D點與點B重合,不合題意.
②若AD=DE時,△ABD與△DCE的相似比為1,此時△ABD≌△DCE,
于是AB=AC=2,BC=2![]() ,AE=AC﹣EC=2﹣BD=2﹣(2
,AE=AC﹣EC=2﹣BD=2﹣(2![]() ﹣2)=4﹣2
﹣2)=4﹣2![]()
③若AE=DE,此時∠DAE=∠ADE=45°,
如下圖所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三線合一可知:AE=CE=![]() AC=1.
AC=1.


 鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學出版社系列答案
鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,一次函數(shù)y1=kx+b的圖象與反比例函數(shù)![]() 的圖象交于點A(﹣2,﹣5),C(5,n),交y軸于點B,交x軸于點D.
的圖象交于點A(﹣2,﹣5),C(5,n),交y軸于點B,交x軸于點D.
(1)求反比例函數(shù)![]() 和一次函數(shù)y1=kx+b的表達式;
和一次函數(shù)y1=kx+b的表達式;
(2)連接OA,OC,求△AOC的面積;
(3)根據(jù)圖象,直接寫出y1>y2時x的取值范圍.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
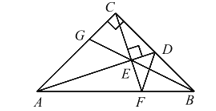
【題目】如圖:Rt△ABC 中,AC=BC,∠ACB=90°,D 為 BC 邊中點,CF⊥AD 交 AD 于 E,交 AB 于 F,BE交 AC 于 G,連 DF,下列結(jié)論:①AC=AF,②CD+DF=AD,③∠ADC=∠BDF,④CE=BE,⑤∠ BED=45°,其中正確的有( )
A. 5 個B. 4 個C. 3 個D. 2 個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】計算
我區(qū)在一項工程招標時,接到甲、乙兩個工程隊的投標書,從投標書中得知:每施工一天,甲工程隊要![]() 萬元,乙工程隊要
萬元,乙工程隊要![]() 萬元,工程小組根據(jù)甲、乙兩隊標書的測算,有三種方案:
萬元,工程小組根據(jù)甲、乙兩隊標書的測算,有三種方案:![]() 甲隊單獨完成這個工程,剛好如期完成;
甲隊單獨完成這個工程,剛好如期完成;![]() 乙隊單獨完成這個工程要比規(guī)定時間多用5天;
乙隊單獨完成這個工程要比規(guī)定時間多用5天;![]() **********,剩下的工程由乙隊單獨做,也正好如期完成. 方案
**********,剩下的工程由乙隊單獨做,也正好如期完成. 方案![]() 中“星號”部分被損毀了. 已知,一個同學設(shè)規(guī)定的工期為
中“星號”部分被損毀了. 已知,一個同學設(shè)規(guī)定的工期為![]() 天,根據(jù)題意列出方程:
天,根據(jù)題意列出方程:![]()
(1)請將方案中“星號”部分補充出來________________;
(2)你認為哪個方案節(jié)省工程款,請說明你的理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
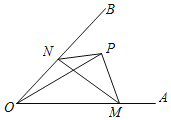
【題目】如圖,∠AOB=45°,點P是∠AOB內(nèi)的定點且OP=![]() ,若點M、N分別是射線OA、OB上異于點O的動點,則△PMN周長的最小值是_____.
,若點M、N分別是射線OA、OB上異于點O的動點,則△PMN周長的最小值是_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(本小題滿分9分)
為了考察甲、乙兩種成熟期小麥的株高長勢狀況,現(xiàn)從中各隨機抽取6株,并測得它們的株高(單位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)請分別計算表內(nèi)兩組數(shù)據(jù)的方差,并借此比較哪種小麥的株高長勢比較整齊?
(2)現(xiàn)將進行兩種小麥優(yōu)良品種雜交試驗,需從表內(nèi)的甲、乙兩種小麥中,各隨機抽取一株進行配對,以預估整體配對狀況.請你用列表法或畫樹狀圖的方法,求所抽取的兩株配對小麥株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,過一點分別作坐標軸的垂線,若與坐標軸圍成矩形的周長的數(shù)值與面積的數(shù)值相等,則這個點叫做和諧點.例如,圖中過點![]() 分別作
分別作![]() 軸,
軸,![]() 軸的垂線.與坐標軸圍成矩形
軸的垂線.與坐標軸圍成矩形![]() 的周長的數(shù)值與面積的數(shù)值相等,則點
的周長的數(shù)值與面積的數(shù)值相等,則點![]() 是和諧點.
是和諧點.

(1)判斷點![]() ,
,![]() 是否為和諧點,并說明理由;
是否為和諧點,并說明理由;
(2)若和諧點![]() 在直線
在直線![]() (
(![]() 為常數(shù))上,求
為常數(shù))上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知![]() 為等邊三角形,
為等邊三角形,![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 、點
、點![]() 重合)以
重合)以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,連接
,連接![]() .
.
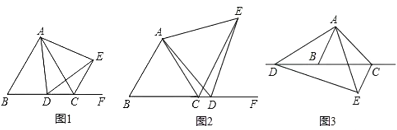
(1)如圖①,當點![]() 在邊
在邊![]() 上時,且點
上時,且點![]() 、點
、點![]() 在
在![]() 同側(cè),其他條件不變,求證:
同側(cè),其他條件不變,求證:![]() ;
;
(2)如圖②,當點![]() 在邊
在邊![]() 的延長線上時,且點
的延長線上時,且點![]() 、點
、點![]() 在
在![]() 同側(cè),其他條件不變,請直接寫出線段
同側(cè),其他條件不變,請直接寫出線段![]() ,
,![]() ,
,![]() 之間存在的數(shù)量關(guān)系,不需證明;
之間存在的數(shù)量關(guān)系,不需證明;
(3)如圖③,當點![]() 在邊
在邊![]() 的延長線上時,且點
的延長線上時,且點![]() 、點
、點![]() 分別在直線
分別在直線![]() 的異側(cè),其他條件不變,請直接寫出線段
的異側(cè),其他條件不變,請直接寫出線段![]() ,
,![]() ,
,![]() 之間存在的數(shù)量關(guān)系,不需證明.
之間存在的數(shù)量關(guān)系,不需證明.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 為一邊.在△ABC 外部作等腰直角三角形ACD ,則線段 BD 的長為_____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com