
【題目】(1)問題發現
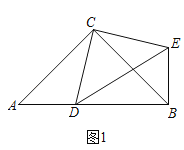
如圖1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,點D時線段AB上一動點,連接BE.
填空:①![]() 的值為 ; ②∠DBE的度數為 .
的值為 ; ②∠DBE的度數為 .
(2)類比探究
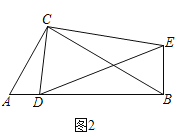
如圖2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,點D是線段AB上一動點,連接BE.請判斷![]() 的值及∠DBE的度數,并說明理由;
的值及∠DBE的度數,并說明理由;
(3)拓展延伸
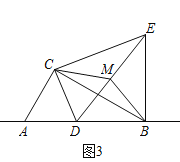
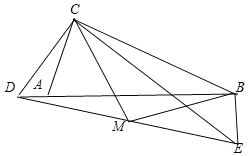
如圖3,在(2)的條件下,將點D改為直線AB上一動點,其余條件不變,取線段DE的中點M,連接BM、CM,若AC=2,則當△CBM是直角三角形時,線段BE的長是多少?請直接寫出答案.
【答案】(1)①1; ②90°;(2)![]() =
=![]() ,∠DBE=90°,理由見解析;(3)BE的長為3+
,∠DBE=90°,理由見解析;(3)BE的長為3+![]() 或3﹣
或3﹣![]()
【解析】
(1)由直角三角形的性質可得∠ABC=45°,可得∠DBE=90°,通過證明△ACD∽△BCE,可得![]() 的值;
的值;
(2)通過證明△ACD∽△BCE,可得![]() 的值,∠CBE=∠CAD=60°,即可求∠DBE的度數;
的值,∠CBE=∠CAD=60°,即可求∠DBE的度數;
(3)分點D在線段AB上和BA延長線上兩種情況討論,由直角三角形的性質可證CM=BM=![]() ,即可求DE=2
,即可求DE=2![]() ,由相似三角形的性質可得∠ABE=90°,BE=
,由相似三角形的性質可得∠ABE=90°,BE=![]() AD,由勾股定理可求BE的長.
AD,由勾股定理可求BE的長.
解:(1)∵∠ACB=90°,∠CAB=45°,
∴∠ABC=∠CAB=45°,
∴AC=BC,∠DBE=∠ABC+∠CBE=90°,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,且∠CAB=∠CDE=45°,
∴△ACD∽△BCE,
∴![]() ,
,
故答案為:1,90°;
(2)![]() ,∠DBE=90°;
,∠DBE=90°;
理由:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴∠ACD=∠BCE,∠CED=∠ABC=30°,
∴tan∠ABC=tan30°=![]() =
=![]() ,
,
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴Rt△ACB∽Rt△DCE,
∴![]() ,
,
∴![]() ,且∠ACD=∠BCE,
,且∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() =
=![]() ,∠CBE=∠CAD=60°,
,∠CBE=∠CAD=60°,
∴∠DBE=∠ABC+∠CBE=90°;
(3)若點D在線段AB上,如圖,
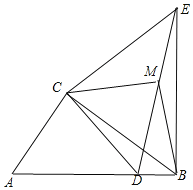
由(2)知:![]() =
=![]() ,∠ABE=90°,
,∠ABE=90°,
∴BE=![]() AD,
AD,
∵AC=2,∠ACB=90°,∠CAB=90°,
∴AB=4,BC=2![]() ,
,
∵∠ECD=∠ABE=90°,且點M是DE中點,
∴CM=BM=![]() DE,
DE,
且△CBM是直角三角形,
∴CM2+BM2=BC2=(2![]() )2,
)2,
∴BM=CM=![]() ,
,
∴DE=2![]() ,
,
∵DB2+BE2=DE2,
∴(4﹣AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() +1,
+1,
∴BE=![]() AD=3+
AD=3+![]() ;
;
若點D在線段BA延長線上,如圖,
同理可得:DE=2![]() ,BE=
,BE=![]() AD,
AD,
∵BD2+BE2=DE2,
∴(4+AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() ﹣1,
﹣1,
∴BE=![]() AD=3﹣
AD=3﹣![]() ,
,
綜上所述:BE的長為3+![]() 或3﹣
或3﹣![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的頂點坐標為
的頂點坐標為![]() ,
,![]() .
.
(1)若該函數圖象過點![]() .
.
①求該函數解析式;
②![]() ,函數圖象上點
,函數圖象上點![]() 到x軸的距離最小值為1,則t的值為______;
到x軸的距離最小值為1,則t的值為______;
(2)若點P在函數![]() 的圖象上,且
的圖象上,且![]() ,求h的最大值.
,求h的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
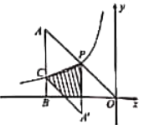
【題目】如圖點P為雙曲線![]() 上一動點.連接OP并延長到點A,使
上一動點.連接OP并延長到點A,使![]() ,過點A作x軸的垂線,垂足為B,交雙曲線于點C.當
,過點A作x軸的垂線,垂足為B,交雙曲線于點C.當![]() 時,連接PC,將
時,連接PC,將![]() 沿直線PC進行翻折,則翻折后的
沿直線PC進行翻折,則翻折后的![]() 與四邊形BOPC的重疊部分(圖中陰影部分)的面積是_______________
與四邊形BOPC的重疊部分(圖中陰影部分)的面積是_______________
查看答案和解析>>
科目:初中數學 來源: 題型:
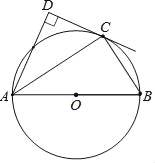
【題目】如圖,點C在以AB為直徑的⊙O上,AD與過點C的切線垂直,垂足為點D.
(1)求證:AC平分∠DAB;
(2)求證:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求線段BC的長.
,求線段BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,∠BAC的平分線交BC于點D,以D為圓心,D長為半徑作作⊙D.
⑴求證:AC是⊙D的切線.
⑵設AC與⊙D切于點E,DB=1,連接DE,BF,EF.
①當∠BAD= 時,四邊形BDEF為菱形;
②當AB= 時,△CDE為等腰三角形.
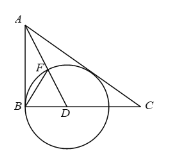
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,P是BC上一動點,過P作AP的垂線交CD于E,將
,P是BC上一動點,過P作AP的垂線交CD于E,將![]() 翻折得到
翻折得到![]() ,延長FP交AB于H,連結AE,PE交AC于G.
,延長FP交AB于H,連結AE,PE交AC于G.

(1)求證![]() ;
;
(2)當![]() 時,求AE的長;
時,求AE的長;
(3)當![]() 時,求AG的長.
時,求AG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求證:對于任意實數m,方程總有兩個不相等的實數根;
(2)若方程的一個根是1,求m的值及方程的另一個根.
查看答案和解析>>
科目:初中數學 來源: 題型:
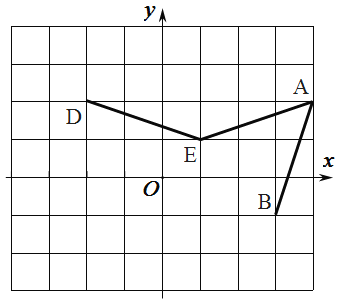
【題目】如圖,在邊長為1的正方形網格中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() 得
得![]() (點
(點![]() 與點
與點![]() 對應).
對應).
(1)直接寫出![]() 的值:
的值:![]() ;
;
(2)用無刻度直尺作出點![]() 并直接寫出
并直接寫出![]() 的坐標(保留作圖痕跡,不寫作法);
的坐標(保留作圖痕跡,不寫作法);
(3)若格點![]() 在
在![]() 的角平分線上,這樣的格點
的角平分線上,這樣的格點![]() (不包括點
(不包括點![]() 有) 個(直接寫出答案)
有) 個(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在電線桿上的C處引拉線CE、CF固定電線桿,拉線CE和地面成60°角,在離電線桿6米的B處安置測角儀,在A處測得電線桿上C處的仰角為30°,已知測角儀高AB為1.5米,求拉線CE的長(結果保留根號).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com