
【題目】已知,如圖,![]() ,垂足分別為
,垂足分別為![]() 、
、![]() ,
,![]() ,試說明
,試說明![]() .
.
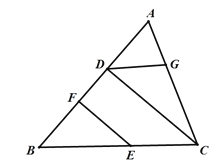
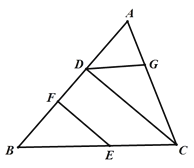
將下面的解答過程補(bǔ)充完整,并填空(理由或數(shù)學(xué)式)
解:∵![]() ,
,![]() (_______________),
(_______________),
∴![]() ______(______________________),
______(______________________),
∴![]() _________(____________________)
_________(____________________)
又∵![]() (已知),
(已知),
∴![]() ________(_____________________),
________(_____________________),
∴![]() _______(_____________________),
_______(_____________________),
∴![]() (_____________________)
(_____________________)
【答案】已知;在同一平面內(nèi),垂直于同一條直線的兩條直線平行;∠BCD(兩直線平行,同位角相等);DG(同旁內(nèi)角互補(bǔ),兩直線平行);∠BCD(兩直線平行,內(nèi)錯角相等);∠CDG(等量代換).
【解析】
根據(jù)垂直定義和平行線的判定推出EF∥CD,推出∠BEF=∠BCD,根據(jù)平行線的判定推出BC∥DG,根據(jù)平行線的性質(zhì)得出∠CDG=∠BCD即可.
∵![]() ,
,![]() (已知),
(已知),
∴EF∥CD_(在同一平面內(nèi),垂直于同一條直線的兩條直線平行),
∴![]() ∠BCD(兩直線平行,同位角相等)
∠BCD(兩直線平行,同位角相等)
又∵![]() (已知),
(已知),
∴![]() DG(同旁內(nèi)角互補(bǔ),兩直線平行),
DG(同旁內(nèi)角互補(bǔ),兩直線平行),
∴![]() ∠BCD(兩直線平行,內(nèi)錯角相等)
∠BCD(兩直線平行,內(nèi)錯角相等)
∵![]() ∠BCD(已證),
∠BCD(已證),
∴![]() ∠CDG(等量代換).
∠CDG(等量代換).


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】七年級二班的幾位同學(xué)正在一起討論一個關(guān)于數(shù)軸上的點(diǎn)表示數(shù)的題目:
甲說:“這條數(shù)軸上的兩個點(diǎn)![]() 、
、![]() 表示的數(shù)都是絕對值是4的數(shù)”;
表示的數(shù)都是絕對值是4的數(shù)”;
乙說:“點(diǎn)![]() 表示負(fù)整數(shù),點(diǎn)
表示負(fù)整數(shù),點(diǎn)![]() 表示正整數(shù),且這兩個數(shù)的差是3”;
表示正整數(shù),且這兩個數(shù)的差是3”;
丙說:“點(diǎn)![]() 表示的數(shù)的相反數(shù)是它本身”.
表示的數(shù)的相反數(shù)是它本身”.
(1)請你根據(jù)以上三位同學(xué)的發(fā)言,畫出一條數(shù)軸,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個不同的點(diǎn).
五個不同的點(diǎn).
(2)求這個五個點(diǎn)表示的數(shù)的和.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
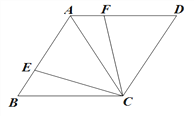
【題目】如圖,四邊形ABCD中,∠B=60°,對角線AC=BC,點(diǎn)E在AB上,將CE繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60得CF,且點(diǎn)F在AD上.
(1)求證:AF=BE;
(2)若AE=DF,求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
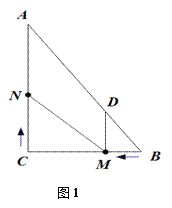
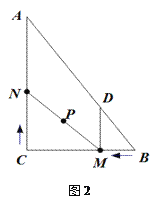
【題目】如圖1,在Rt△ABC中,∠C=90,BC=6,AC=8.動點(diǎn)M從點(diǎn)B開始沿邊BC向點(diǎn)C以每秒1個單位長度的速度運(yùn)動,動點(diǎn)N從點(diǎn)C開始沿邊CA向點(diǎn)A以每秒2個單位長度的速度運(yùn)動,點(diǎn)M、N同時(shí)出發(fā),且當(dāng)其中一點(diǎn)到達(dá)端點(diǎn)時(shí),另一點(diǎn)也隨之停止運(yùn)動.過點(diǎn)M作MD∥AC,交AB于點(diǎn)D,連接MN.設(shè)運(yùn)動時(shí)間為t秒(t≥0).
(1)當(dāng)t為何值時(shí),四邊形ADMN為平行四邊形?
(2)是否存在t的值,使四邊形ADMN為菱形?若存在,求出t的值;若不存在,說明理由.并探究只改變點(diǎn)N的速度(勻速運(yùn)動),使四邊形ADMN在某一時(shí)刻為菱形,求點(diǎn)N的速度;
(3)如圖2,在整個運(yùn)動過程中,求出線段MN中點(diǎn)P所經(jīng)過的路徑長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB∥CD,EF與AB,CD分別交于點(diǎn)G,H,∠CHG的平分線HM交AB于點(diǎn)M,若∠EGB=50°,則∠GMH的度數(shù)為( )
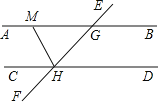
A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
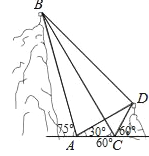
【題目】如圖,B,D為兩島上的兩座燈塔的塔頂,測量船于水面A處測得B點(diǎn)和D點(diǎn)的仰角分別為75°,30°.于水面C處測得B點(diǎn)和D點(diǎn)的仰角均為60°,AC=0.1km.
(1)試探究圖中B,D間距離與另外哪兩點(diǎn)間距離相等;
(2)求B點(diǎn)距水平面的高度(計(jì)算結(jié)果精確到0.01km,參考數(shù)據(jù):![]() ≈1.73,tan75°≈3.73)
≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在平面直角坐標(biāo)系中,A點(diǎn)坐標(biāo)為(-2,2).
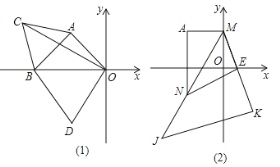
⑴如圖⑴,在△ABO為等腰直角三角形,求B點(diǎn)坐標(biāo).
⑵如圖⑴,在⑴的條件下,分別以AB和OB為邊作等邊△ABC和等邊△OBD,連結(jié)OC,求∠COB的度數(shù).
⑶如圖⑵,過點(diǎn)A作AM⊥y軸于點(diǎn)M,點(diǎn)E為x軸正半軸上一點(diǎn),K為ME延長線上一點(diǎn),以MK為直角邊作等腰直角三角形MKJ,∠MKJ=90°,過點(diǎn)A作AN⊥x軸交MJ于點(diǎn)N,連結(jié)EN.則①![]() 的值不變;②
的值不變;②![]() 的值不變,其中有且只有一個結(jié)論正確,請判斷出正確的結(jié)論,并加以證明和求出其值.
的值不變,其中有且只有一個結(jié)論正確,請判斷出正確的結(jié)論,并加以證明和求出其值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
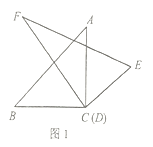
(1)如圖1,將頂點(diǎn)![]() 和頂點(diǎn)
和頂點(diǎn)![]() 重合,保持三角板
重合,保持三角板![]() 不動,將三角板
不動,將三角板![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn).當(dāng)
旋轉(zhuǎn).當(dāng)![]() 平分
平分![]() 時(shí),求
時(shí),求![]() 的度數(shù);
的度數(shù);
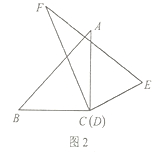
(2)在(1)的條件下,繼續(xù)旋轉(zhuǎn)三角板![]() ,猜想
,猜想![]() 與
與![]() 有怎樣的數(shù)量關(guān)系?并利用圖2所給的情形說明理由;
有怎樣的數(shù)量關(guān)系?并利用圖2所給的情形說明理由;
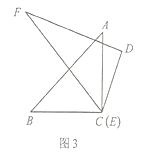
(3)如圖3,將頂點(diǎn)![]() 和頂點(diǎn)
和頂點(diǎn)![]() 重合,保持三角板
重合,保持三角板![]() 不動,將三角板
不動,將三角板![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn).當(dāng)
旋轉(zhuǎn).當(dāng)![]() 落在
落在![]() 內(nèi)部時(shí),直接寫出
內(nèi)部時(shí),直接寫出![]() 與
與![]() 的數(shù)量關(guān)系.
的數(shù)量關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
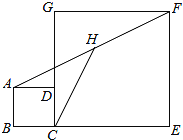
【題目】如圖,正方形ABCD和正方形CEFG中,點(diǎn)D在CG上,已知:BC=1,CE=7,H是AF的中點(diǎn),則AF=_____,CH=_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com