
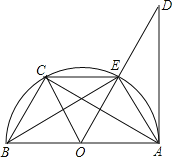
【題目】如圖,已知AB是⊙O的直徑,AD切⊙O于點A,點C是![]() 的中點,則下列結論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )
的中點,則下列結論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )
A.1個B.2個C.3個D.4個
【答案】C
【解析】
由C為弧EB中點,利用垂徑定理的逆定理得到OC垂直于BE,根據等弧對等弦得到BC=EC,再由AB為直角,利用圓周角定理得到AE垂直于BE,進而得到一對直角相等,利用同位角相等兩直線平行得到OC與AE平行,由AD為圓的切線,利用切線的性質得到AB與DA垂直,利用同角的余角相等得到∠DAE=∠ABE,根據E不一定為弧AC中點,可得出AC與OE不一定垂直,即可確定出結論成立的序號.
解:∵C為![]() 的中點,即
的中點,即![]() ,
,
∴OC⊥BE,BC=EC,選項②正確;
設AE與CO交于F,∴∠BFO=90°,
∵AB為圓O的直徑,
∴AE⊥BE,即∠BEA=90°,
∴∠BFO=∠BEA,
∴OC∥AE,選項①正確;
∵AD為圓的切線,
∴∠DAB=90°,即∠DAE+∠EAB=90°,
∵∠EAB+∠ABE=90°,
∴∠DAE=∠ABE,選項③正確;
點E不一定為![]() 中點,故E不一定是
中點,故E不一定是![]() 中點,選項④錯誤,
中點,選項④錯誤,
則結論成立的是①②③,
故選:C.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:
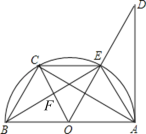
【題目】如圖,AB是⊙O的直徑,點C是![]() 的中點,連接AC并延長至點D,使CD=AC,點E是OB上一點,且
的中點,連接AC并延長至點D,使CD=AC,點E是OB上一點,且![]() ,CE的延長線交DB的延長線于點F,AF交⊙O于點H,連接BH.
,CE的延長線交DB的延長線于點F,AF交⊙O于點H,連接BH.

(1)求證:BD是⊙O的切線;(2)當OB=2時,求BH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一場足球比賽中,一球員從球門正前方10米處起腳射門,當球飛行的水平距離為6米時達到最高點,此時球高為3米.
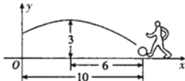
(1)如圖建立直角坐標系,當球飛行的路線為一拋物線時,求此拋物線的解析式.
(2)已知球門高為2.44米,問此球能否射中球門(不計其它情況).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,∠A=60°,點D是線段BC的中點,∠EDF=120°,DE與線段AB相交于點E,DF與線段AC(或AC的延長線)相交于點F.
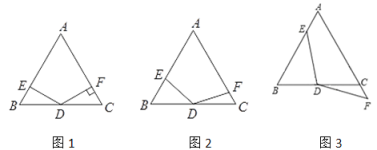
(1)如圖1,若DF⊥AC,垂足為F,證明:DE=DF
(2)如圖2,將∠EDF繞點D順時針旋轉一定的角度,DF仍與線段AC相交于點F.DE=DF仍然成立嗎?說明理由.
(3)如圖3,將∠EDF繼續繞點D順時針旋轉一定的角度,使DF與線段AC的延長線相交于點F,DE=DF仍然成立嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人民生活水平的不斷提高,龍崗區家庭轎車的擁有量逐年增加.據統計,某小區2017年底擁有家庭轎車81輛,2019年底家庭轎車的擁有量達到144輛.
(1)若該小區2017年底到2019年底家庭轎車擁有量的年平均增長率都相同,求該小區到2020年底家庭轎車將達到多少輛?
(2)為了緩解停車矛盾,該小區決定投資25萬元再建造若干個停車位.據測算,建造費用分別為室內車位6000元/個,露天車位2000元/個,考慮到實際因素,計劃露天車位的數量不少于室內車位的3倍,但不超過室內車位的4.5倍,求該小區最多可建兩種車位各多少個?試寫出所有可能的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小正方形的邊長都是單位1,△ABC的三個頂點都在格點上,結合所給的平面直角坐標系解答下列問題:
(1)將△ABC向上平移3個單位長度,畫出平移后的△A1B1C1;
(2)寫出A1、C1的坐標;
(3)將△A1B1C1繞B1逆時針旋轉90°,畫出旋轉后的△A2B1C2,求線段B1C1旋轉過程中掃過的面積(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中點O為圓心,作半圓與DE相切,點A、B分別是半圓和邊DF上的動點,連接AB,則AB的最大值與最小值的和是( )

A.6B.2![]() +1C.
+1C.![]() D.9
D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,M、N分別是射線CB和射線DC上的動點,且始終∠MAN=45°.

(1)如圖1,當點M、N分別在線段BC、DC上時,請直接寫出線段BM、MN、DN之間的數量關系;
(2)如圖2,當點M、N分別在CB、DC的延長線上時,(1)中的結論是否仍然成立,若成立,給予證明,若不成立,寫出正確的結論,并證明;
(3)如圖3,當點M、N分別在CB、DC的延長線上時,若CN=CD=6,設BD與AM的延長線交于點P,交AN于Q,直接寫出AQ、AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假快要到了,某市準備組織同學們分別到A,B,C,D四個地方進行夏令營活動,前往四個地方的人數如圖所示.
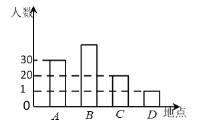
(1)去B地參加夏令營活動人數占總人數的40%,根據統計圖求去B地的人數?
(2)若一對姐弟中只能有一人參加夏令營,姐弟倆提議讓父親決定.父親說:現有4張卡片上分別寫有1,2,3,4四個整數,先讓姐姐隨機地抽取一張后放回,再由弟弟隨機地抽取一張.若抽取的兩張卡片上的數字之和是5的倍數則姐姐參加,若抽取的兩張卡片上的數字之和是3的倍數則弟弟參加.用列表法或樹形圖分析這種方法對姐弟倆是否公平?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com