
【題目】如圖,在![]() 中,
中,![]() 、
、![]() 是對角線
是對角線![]() 上兩點,
上兩點,![]() ,
,![]() ,
,![]() ,則
,則![]() 的大小為___________
的大小為___________
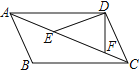
【答案】21°.
【解析】
由直角三角形斜邊中線的性質得DE=AE=EF,進而可得DC=DE,設∠ADE=x,則∠DAE=x,進而可得∠DCE=∠DEC=2x,再根據(jù)平行線的性質可得 ∠ACB=∠DAE=x,再根據(jù)∠ACB+∠ACD=∠BCD=63°,即可求得答案.
∵AE=EF,∠ADF=90°,
∴DE=AE=EF,
∴∠DAE=∠ADE,
又∵AE=EF=CD,
∴DC=DE,
∴∠DEC=∠DCE,
設∠ADE=x,則∠DAE=x,
則∠DCE=∠DEC=2x,
又AD∥BC,
∴∠ACB=∠DAE=x,
由∠ACB+∠ACD=∠BCD=63°,
得:x+2x=63°,
解得:x=21°,
∴∠ADE=21°,
故答案為:21°.


科目:初中數(shù)學 來源: 題型:
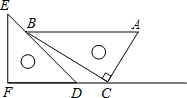
【題目】三角板是我們學習數(shù)學的好幫手.將一對直角三角板如圖放置,點C在FD的延長線上,點B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,則CD的長度是_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為迎接“世界華人炎帝故里尋根節(jié)”,某工廠接到一批紀念品生產(chǎn)訂單,按要求在15天內完成,約定這批紀念品的出廠價為每件20元,設第x天(1≤x≤15,且x為整數(shù))每件產(chǎn)品的成本是p元,p與x之間符合一次函數(shù)關系,部分數(shù)據(jù)如表:
天數(shù)(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任務完成后,統(tǒng)計發(fā)現(xiàn)工人李師傅第x天生產(chǎn)的產(chǎn)品件數(shù)y(件)與x(天)滿足如下關系:y=![]() ,
,
設李師傅第x天創(chuàng)造的產(chǎn)品利潤為W元.
(1)直接寫出p與x,W與x之間的函數(shù)關系式,并注明自變量x的取值范圍:
(2)求李師傅第幾天創(chuàng)造的利潤最大?最大利潤是多少元?
(3)任務完成后.統(tǒng)計發(fā)現(xiàn)平均每個工人每天創(chuàng)造的利潤為299元.工廠制定如下獎勵制度:如果一個工人某天創(chuàng)造的利潤超過該平均值,則該工人當天可獲得20元獎金.請計算李師傅共可獲得多少元獎金?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
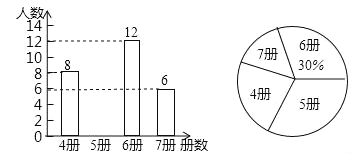
【題目】高爾基說:“書,是人類進步的階梯.”閱讀可以豐富知識、拓展視野、充實生活等諸多益處.為了解學生的課外閱讀情況,某校隨機抽查了部分學生閱讀課外書冊數(shù)的情況,并繪制出如下統(tǒng)計圖,其中條形統(tǒng)計圖因為破損丟失了閱讀5冊書數(shù)的數(shù)據(jù).
(1)求條形圖中丟失的數(shù)據(jù),并寫出閱讀書冊數(shù)的眾數(shù)和中位數(shù);
(2)根據(jù)隨機抽查的這個結果,請估計該校1200名學生中課外閱讀5冊書的學生人數(shù);
(3)若學校又補查了部分同學的課外閱讀情況,得知這部分同學中課外閱讀最少的是6冊,將補查的情況與之前的數(shù)據(jù)合并后發(fā)現(xiàn)中位數(shù)并沒有改變,試求最多補查了多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
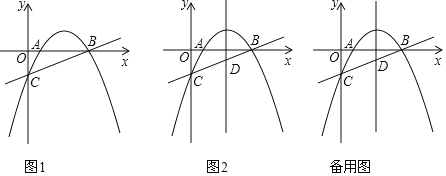
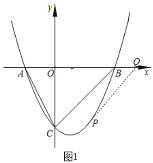
【題目】如圖,直線![]() 與x軸、y軸分別交于BC兩點,拋物線
與x軸、y軸分別交于BC兩點,拋物線![]() 經(jīng)過B、C兩點,且與x軸交于點A
經(jīng)過B、C兩點,且與x軸交于點A
(1)求該拋物線的函數(shù)表達式;
(2)已知點M是第一象限內拋物線上的一個動點,過點M作MN平行于y軸交直線BC于點N,連接AM、BM、AN,求四邊形MANB面積S的最大值,并求出此時點M的坐標;
(3)拋物線的對稱軸交直線BC于點D,若Q為y軸上一點,則在拋物線上是否存在一點P,使得以B、D、P、Q為頂點的四邊形是平行四邊形?若存在,直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
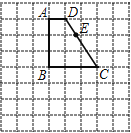
【題目】如圖是由邊長為1的小正方形構成的網(wǎng)格,每個小正方形的頂點叫做格點.四邊形![]() 的頂點在格點上,點
的頂點在格點上,點![]() 是邊
是邊![]() 與網(wǎng)格線的交點.請選擇適當?shù)母顸c,用無刻度的直尺在網(wǎng)格中完成下列畫圖,保留連線的痕跡,不要求說明理由
與網(wǎng)格線的交點.請選擇適當?shù)母顸c,用無刻度的直尺在網(wǎng)格中完成下列畫圖,保留連線的痕跡,不要求說明理由
(1)如圖1,過點![]() 畫線段
畫線段![]() ,使
,使![]() ,且
,且![]()
(2)如圖1,在邊![]() 上畫一點
上畫一點![]() ,使
,使![]()
(3)如圖2,過點![]() 畫線段
畫線段![]() ,使
,使![]() ,且
,且![]()

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商場為了抓住夏季來臨,襯衫熱銷的契機,決定用46000元購進![]() 、
、![]() 、
、![]() 三種品牌的襯衫共300件,并且購進的每一種襯衫的數(shù)量都不少于90件.設購進
三種品牌的襯衫共300件,并且購進的每一種襯衫的數(shù)量都不少于90件.設購進![]() 種型號的襯衣
種型號的襯衣![]() 件,購進
件,購進![]() 種型號的襯衣
種型號的襯衣![]() 件,三種品牌的襯衫的進價和售價如下表所示:
件,三種品牌的襯衫的進價和售價如下表所示:
型號 |
|
|
|
進價(元/件) | 100 | 200 | 150 |
售價(元/件) | 200 | 350 | 300 |
(Ⅰ)直接用含![]() 、
、![]() 的代數(shù)式表示購進
的代數(shù)式表示購進![]() 種型號襯衣的件數(shù),其結果可表示為______;
種型號襯衣的件數(shù),其結果可表示為______;
(Ⅱ)求![]() 與
與![]() 之間的函數(shù)關系式;
之間的函數(shù)關系式;
(Ⅲ)如果該商場能夠將購進的襯衫全部售出,但在銷售這些襯衫的過程中還需要另外支出各種費用共計1000元.
①求利潤![]() (元)與
(元)與![]() (件)之間的函數(shù)關系式;
(件)之間的函數(shù)關系式;
②求商場能夠獲得的最大利潤.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商店購進![]() 、
、![]() 兩種商品,購買1個
兩種商品,購買1個![]() 商品比購買1個
商品比購買1個![]() 商品多花10元,并且花費300元購買
商品多花10元,并且花費300元購買![]() 商品和花費100元購買
商品和花費100元購買![]() 商品的數(shù)量相等.
商品的數(shù)量相等.
(1)求購買一個![]() 商品和一個
商品和一個![]() 商品各需要多少元;
商品各需要多少元;
(2)商店準備購買![]() 、
、![]() 兩種商品共80個,若
兩種商品共80個,若![]() 商品的數(shù)量不少于
商品的數(shù)量不少于![]() 商品數(shù)量的4倍,并且購買
商品數(shù)量的4倍,并且購買![]() 、
、![]() 商品的總費用不低于1000元且不高于1050元,那么商店有哪幾種購買方案?
商品的總費用不低于1000元且不高于1050元,那么商店有哪幾種購買方案?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() .
.
(1)點![]() 的坐標為__________,點
的坐標為__________,點![]() 的坐標為__________,線段
的坐標為__________,線段![]() 的長為__________,拋物線的解析式為__________.
的長為__________,拋物線的解析式為__________.
(2)點![]() 是線段
是線段![]() 下方拋物線上的一個動點.
下方拋物線上的一個動點.
①如果在![]() 軸上存在點
軸上存在點![]() ,使得以點
,使得以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形.求點
為頂點的四邊形是平行四邊形.求點![]() 的坐標.
的坐標.
②如圖2,過點![]() 作
作![]() 交線段
交線段![]() 于點
于點![]() ,過點
,過點![]() 作直線
作直線![]() 交
交![]() 于點
于點![]() ,交
,交![]() 軸于點
軸于點![]() ,記
,記![]() ,求
,求![]() 關于
關于![]() 的函數(shù)解析式;當
的函數(shù)解析式;當![]() 取
取![]() 和
和![]() 時,試比較
時,試比較![]() 的對應函數(shù)值
的對應函數(shù)值![]() 和
和![]() 的大小.
的大小.
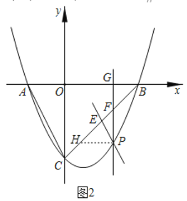
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com