
【題目】如圖,在平面直角坐標系中,二次函數y=ax2+bx+c的圖象經過點A(﹣1,0),B(0,﹣ ![]() ),C(2,0),其對稱軸與x軸交于點D
),C(2,0),其對稱軸與x軸交于點D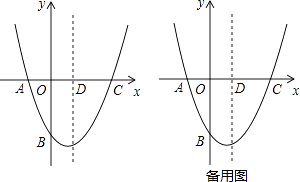
(1)求二次函數的表達式及其頂點坐標;
(2)若P為y軸上的一個動點,連接PD,則 ![]() PB+PD的最小值為;
PB+PD的最小值為;
(3)M(x,t)為拋物線對稱軸上一動點
①若平面內存在點N,使得以A,B,M,N為頂點的四邊形為菱形,則這樣的點N共有 個;
②連接MA,MB,若∠AMB不小于60°,求t的取值范圍.
【答案】
(1)
解:由題意 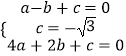 解得
解得 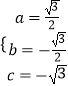 ,
,
∴拋物線解析式為y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∵y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴頂點坐標( ![]() ,﹣
,﹣ ![]() )
)
(2)![]()
(3)
① 5
②解:如圖,RT△AOB中,∵tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
作AB的中垂線與y軸交于點E,連接EA,則∠AEB=120°,
以E為圓心,EB為半徑作圓,與拋物線對稱軸交于點F、G.
則∠AFB=∠AGB=60°,從而線段FG上的點滿足題意,
∵EB= ![]() =
= ![]() ,
,
∴OE=OB﹣EB= ![]() ,
,
∵F( ![]() ,t),EF2=EB2,
,t),EF2=EB2,
∴( ![]() )2+(t+
)2+(t+ ![]() )2=(
)2=( ![]() )2,
)2,
解得t= ![]() 或
或 ![]() ,
,
故F( ![]() ,
, ![]() ),G(
),G( ![]() ,
, ![]() ),
),
∴t的取值范圍 ![]() ≤t≤
≤t≤ ![]()
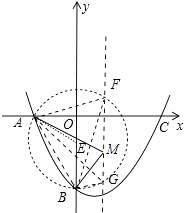
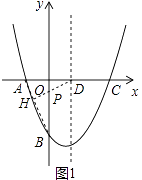
【解析】【解析】解:(2)如圖1中,連接AB,作DH⊥AB于H,交OB于P,
此時 ![]() PB+PD最小.
PB+PD最小.
理由:∵OA=1,OB= ![]() ,
,
∴tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
∴PH= ![]() PB,
PB,
∴ ![]() PB+OD=PH+PD=DH,
PB+OD=PH+PD=DH,
∴此時 ![]() PB+PD最短(垂線段最短).
PB+PD最短(垂線段最短).
在RT△ADH中,∵∠AHD=90°,AD= ![]() ,∠HAD=60°,
,∠HAD=60°,
∴sin60°= ![]() ,
,
∴DH= ![]() ,
,
∴ ![]() PB+PD的最小值為
PB+PD的最小值為 ![]() .
.
所以答案是 ![]() .
.
(3)①以A為圓心AB為半徑畫弧與對稱軸有兩個交點,
以B為圓心AB為半徑畫弧與對稱軸也有兩個交點,
線段AB的垂直平分線與對稱軸有一個交點,
所以滿足條件的點M有5個,即滿足條件的點N也有5個,
所以答案是5.
(1)利用待定系數法轉化為解方程組解決問題.(2)如圖1中,連接AB,作DH⊥AB于H,交OB于P,此時 ![]() PB+PD最小.最小值就是線段DH,求出DH即可.(3)①先在對稱軸上尋找滿足△ABM是等腰三角形的點M,由此即可解決問題.②作AB的中垂線與y軸交于點E,連接EA,則∠AEB=120°,以E為圓心,EB為半徑作圓,與拋物線對稱軸交于點F、G.則∠AFB=∠AGB=60°,從而線段FG上的點滿足題意,求出F、G的坐標即可解決問題.本題考查二次函數綜合題、銳角三角函數、最短問題、圓等知識,解題的關鍵是掌握待定系數法確定函數解析式,學會利用垂線段最短解決實際問題中的最短問題,學會添加輔助線,構造圓解決角度問題,屬于中考壓軸題.
PB+PD最小.最小值就是線段DH,求出DH即可.(3)①先在對稱軸上尋找滿足△ABM是等腰三角形的點M,由此即可解決問題.②作AB的中垂線與y軸交于點E,連接EA,則∠AEB=120°,以E為圓心,EB為半徑作圓,與拋物線對稱軸交于點F、G.則∠AFB=∠AGB=60°,從而線段FG上的點滿足題意,求出F、G的坐標即可解決問題.本題考查二次函數綜合題、銳角三角函數、最短問題、圓等知識,解題的關鍵是掌握待定系數法確定函數解析式,學會利用垂線段最短解決實際問題中的最短問題,學會添加輔助線,構造圓解決角度問題,屬于中考壓軸題.
【考點精析】根據題目的已知條件,利用垂線段最短和銳角三角函數的增減性的相關知識可以得到問題的答案,需要掌握連接直線外一點與直線上各點的所有線段中,垂線段最短;現實生活中開溝引水,牽牛喝水都是“垂線段最短”性質的應用;當角度在0°~90°之間變化時:(1)正弦值隨著角度的增大(或減小)而增大(或減小)(2)余弦值隨著角度的增大(或減小)而減小(或增大)(3)正切值隨著角度的增大(或減小)而增大(或減小)(4)余切值隨著角度的增大(或減小)而減小(或增大).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,線段AB是⊙O的直徑,弦CD⊥AB,∠CAB=40°,則∠ABD與∠AOD分別等于( ) 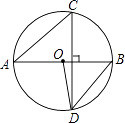
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,∠BAC=90°,AB=AC,點E在AC上(且不與點A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,連接AD,分別以AB,AD為鄰邊作平行四邊形ABFD,連接AF.
(1)請直接寫出線段AF,AE的數量關系;
(2)將△CED繞點C逆時針旋轉,當點E在線段BC上時,如圖②,連接AE,請判斷線段AF,AE的數量關系,并證明你的結論;
(3)在圖②的基礎上,將△CED繞點C繼續逆時針旋轉,請判斷(2)問中的結論是否發生變化?若不變,結合圖③寫出證明過程;若變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于點E,點F在AC上,且BD=DF.
(1)求證:CF=EB;
(2)請你判斷AE、AF與BE之間的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測出旗桿AB的高度,在旗桿前的平地上選擇一點C,測得旗桿頂部A的仰角為45°,在C、B之間選擇一點D(C、D、B三點共線),測得旗桿頂部A的仰角為75°,且CD=8m 
(1)求點D到CA的距離;
(2)求旗桿AB的高.
(注:結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以直角三角形a、b、c為邊,向外作等邊三角形,半圓,等腰直角三角形和正方形,上述四種情況的面積關系滿足S1+S2=S3圖形個數有( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,Rt△ABC中,∠C=90°,BC=6,AC=8.動點P從點A出發沿A—B—C的方向以每秒2個單位的速度運動.設P的運動時間為t(秒).
(1)請直接用含t的代數式表示①當點P在AB上時,BP= ;②當點P在BC上時,BP= ;
(2)求△BPC為等腰三角形的t值.

 (備用圖)
(備用圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某新農村樂園設置了一個秋千場所,如圖所,秋千拉繩OB的長為3m,靜止時,踏板到地面距離BD的長為0.6m(踏板厚度忽略不計).為安全起見,樂園管理處規定:兒童的“安全高度”為hm,成人的“安全高度”為2m(計算結果精確到0.1m) 
(1)當擺繩OA與OB成45°夾角時,恰為兒童的安全高度,則h= 1.5 m
(2)某成人在玩秋千時,擺繩OC與OB的最大夾角為55°,問此人是否安全?(參考數據: ![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我州某養殖場計劃購買甲、乙兩種魚苗600條,甲種魚苗每條16元,乙種魚苗每條20元,相關資料表明:甲、乙兩種魚苗的成活率為80%,90%
(1)若購買這兩種魚苗共用去11000元,則甲、乙兩種魚苗各購買多少條?
(2)若要使這批魚苗的總成活率不低于85%,則乙種魚苗至少購買多少條?
(3)在(2)的條件下,應如何選購魚苗,使購買魚苗的總費用最低?最低費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com