
【題目】定義:①已知A(x1,y1)、B(x2,y2),則AB=![]() ;② 已知A(x0,y0)直線 l 的方程為 Ax By C 0, 則 A 到直線的距離
;② 已知A(x0,y0)直線 l 的方程為 Ax By C 0, 則 A 到直線的距離![]()
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直線l : 3x 4y 5 0,求 A 到直線的距離;
(3)求兩平行直線3x 4y1 0與3x 4 y 8 0之間的距離;
(4)求![]() 的最小值.
的最小值.
【答案】(1)5;(2)3;(3)![]() ;(4)
;(4)![]()
【解析】
(1)由A與B的坐標,利用題中的方法求出AB的長即可;
(2)利用點到直線的距離公式求出A到直線的距離即可;
(3)從直線3x 4y1 0上找一個點,求出該點到3x 4 y 8 0的距離,即為兩條平行線的距離;
(4)先將![]() 轉化成兩點間距離公式
轉化成兩點間距離公式![]() 形式,把原式最小值轉化為兩點間距離問題.
形式,把原式最小值轉化為兩點間距離問題.
解:(1)將A2,5、 B1,1,代入AB=![]()
得:AB=![]()
所以AB長為5;
(2)將A2,1,直線l : 3x 4y 5 0,代入![]()
可得:![]() ,
,
所以A 到直線的距離為3;
(3)在直線3x 4y1 0上取x=1,則y=-1,
∴(1,-1)在直線3x 4y1 0上,
將(1,-1)和3x 4 y 8 0代入![]()
可得:![]()
所以兩平行直線3x 4y1 0與3x 4 y 8 0之間的距離為![]() ;
;
(4)![]()
![]()
![]()
所以原式的值即為點(x,0)到點(-2,-1)和點(3,4)的距離和,
由于點(-2,-1)和點(3,4)位于點(x,0)兩側,
那么原式的最小值即為點(-2,-1)和點(3,4)兩點間的距離,
∵![]()
![]() ,
,
∴![]() 的最小值為
的最小值為![]()


科目:初中數學 來源: 題型:
【題目】在長方形![]() 中,
中,![]() ,現將長方形
,現將長方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到長方形
后到長方形![]() 的位置(
的位置(![]() 的對應點為
的對應點為![]() ,其它類似).
,其它類似).
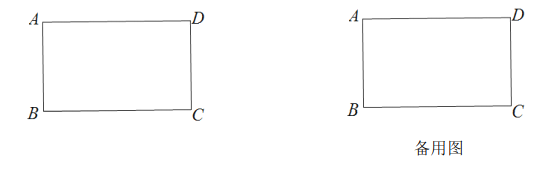
![]() 當
當![]() 時,請畫出平移后的長方形
時,請畫出平移后的長方形![]() ,并求出長方形
,并求出長方形![]() 與長方形
與長方形![]() 的重疊部分的面積.
的重疊部分的面積.
![]() 當
當![]() 滿足什么條件時,長方形
滿足什么條件時,長方形![]() 與長方形
與長方形![]() 有重疊部分(邊與邊疊合不算在內),請用
有重疊部分(邊與邊疊合不算在內),請用![]() 的代數式表示重疊部分的面積.
的代數式表示重疊部分的面積.
![]() 在平移的過程中,總會形成一個六邊形
在平移的過程中,總會形成一個六邊形![]() ,試用
,試用![]() 來表示六邊形
來表示六邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An-1PnAnBn都是正方形,對角線OA1、A1A2、A2A3、……、An-1An都在y軸上(n≥2),點P1(x1,y1),點P2(x2,y2),……,點Pn(xn,yn)在反比例函數y=![]() (x>0)的圖象上,已知B1 (-1,1)。
(x>0)的圖象上,已知B1 (-1,1)。
(1)反比例函數解析式為________;
(2)求點P1和點P2的坐標;
(3)點Pn的坐標為(____________)(用含n的式子表示),△PnBnO的面積為__________。(直接填答案)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游泳館每年夏季推出兩種游泳付費方式,方式一:先購買會員證,每張會員證100元,只限本人當年使用,憑證游泳每次再付費5元;方式二:不購買會員證,每次游泳付費9元.
設小明計劃今年夏季游泳次數為x(x為正整數).
(I)根據題意,填寫下表:
游泳次數 | 10 | 15 | 20 | … | x |
方式一的總費用(元) | 150 | 175 | ______ | … | ______ |
方式二的總費用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明計劃今年夏季游泳的總費用為270元,選擇哪種付費方式,他游泳的次數比較多?
(Ⅲ)當x>20時,小明選擇哪種付費方式更合算?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平行四邊形ABCD中,O為對角線BD的中點,過點O的直線EF分別交AD,BC于E,F兩點,連結BE,DF.
(1)求證:△DOE≌△BOF.
(2)當∠DOE等于多少度時,四邊形BFDE為菱形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區要在一塊長方形的空地上修建三條人行道(陰影部分),其余空地鋪設草坪進行美化,設計規劃如圖所示,長方形空地長為m米,寬為n米,且三條人行道寬均為2米.
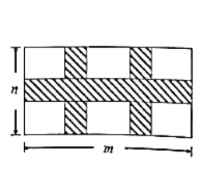
(1)請直接寫出草坪面積是多少平方米?(用m,n表示)
(2)若n=18,且人行道所占面積為整個長方形空地面積的![]() ,則該長方形空地的長為多少米?
,則該長方形空地的長為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新規定:點![]() 為線段
為線段![]() 上一點,當
上一點,當![]() 或
或![]() 時,我們就規定
時,我們就規定![]() 為線段
為線段![]() 的“三倍距點”。如圖,在數軸上,點
的“三倍距點”。如圖,在數軸上,點![]() 所表示的數為-3,點
所表示的數為-3,點![]() 所表示的數為5.
所表示的數為5.

(1)確定點![]() 所表示的數為___________.
所表示的數為___________.
(2)若動點![]() 從點
從點![]() 出發,沿射線
出發,沿射線![]() 方向以每秒2個單位長度的速度運動,設運動時間為
方向以每秒2個單位長度的速度運動,設運動時間為![]() 秒.
秒.
①當點![]() 與點
與點![]() 重合時,求
重合時,求![]() 的值.
的值.
②求![]() 的長度(用含
的長度(用含![]() 的代數式表示).
的代數式表示).
③當點![]() 為線段
為線段![]() 的“三倍距點”時,直接寫出
的“三倍距點”時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]() 給出以下結論:①當a=3時,方程組的解也是方程2x-y=a+13的解;②無論a取何值,x,y的值都不可能互為相反數;③x,y的自然數的解有2對;④若z=
給出以下結論:①當a=3時,方程組的解也是方程2x-y=a+13的解;②無論a取何值,x,y的值都不可能互為相反數;③x,y的自然數的解有2對;④若z=![]() (x+3)y,則z的最大值是36.其中正確的是______.(填序號)
(x+3)y,則z的最大值是36.其中正確的是______.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春暖花開,市民紛紛外出踏青,某種品牌鞋專賣店抓住機遇,利用10周年店慶對其中暢銷的M款運動鞋進行促銷,M款運動鞋每雙的成本價為800元,標價為1200元.
(1)M款運動鞋每雙最多降價多少元,才能使利潤率不低于20%;
(2)該店以前每周共售出M款運動鞋100雙,2017年3月的一個周末,恰好是該店的10周年店慶,這個周末M款運動鞋每雙在標價的基礎上降價 ![]() m%,結果這個周末賣出的M款運動鞋的數量比原來一周賣出的M款運動鞋的數量增加了
m%,結果這個周末賣出的M款運動鞋的數量比原來一周賣出的M款運動鞋的數量增加了 ![]() m%,這周周末的利潤達到了40000元,求m的值.
m%,這周周末的利潤達到了40000元,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com