
【題目】已知二次函數y=x2﹣(2m+1)+( ![]() m2﹣1).
m2﹣1).
(1)求證:不論m取什么實數,該二次函數圖象與x軸總有兩個交點;
(2)若該二次函數圖象經過點(2m﹣2,﹣2m﹣1),求該二次函數的表達式.
【答案】
(1)解:∵b2﹣4ac=(2m+1)2﹣4( ![]() m2﹣1)
m2﹣1)
=(4m2+4m+1)﹣2m2+4
=2m2+4m+5
=2(m+1)2+3>0,
∴不論m取什么實數,方程x2﹣(2m+1)+( ![]() m2﹣1)=0都有兩個不相等的實數根,
m2﹣1)=0都有兩個不相等的實數根,
∴不論m取什么實數,該二次函數圖象與x軸總有兩個交點
(2)解:∵該二次函數圖象經過點(2m﹣2,﹣2m﹣1),
∴(2m﹣2)2﹣(2m+1)(2m﹣2)+( ![]() m2﹣1)=﹣2m﹣1,
m2﹣1)=﹣2m﹣1,
解得:m1=2,m2=6,
當m=2時,該二次函數的表達式為:y=x2﹣5x+1,
當m=6時,該二次函數的表達式為:y=x2﹣13x+17
【解析】(1)首先求出b2﹣4ac的表達式,進而利用配方法求出其符號,進而得出答案;(2)將已知點代入進而求出m的值得出答案.


科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC內部的一個動點,且滿足∠PAB=∠PBC,則線段CP長的最小值為( ) 
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠設門市部專賣某產品,該產品每件成本40元,從開業一段時間的每天銷售統計中,隨機抽取一部分情況如下表所示:
每件銷售價(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
每天售出件數 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假設當天定的售價是不變的,且每天銷售情況均服從這種規律.
(1)觀察這些統計數據,找出每天售出件數y與每件售價x(元)之間的函數關系,并寫出該函數關系式.
(2)門市部原設有兩名營業員,但當銷售量較大時,在每天售出量超過168件時,則必須增派一名營業員才能保證營業有序進行,設營業員每人每天工資為40元.求每件產品應定價多少元,才能使每天門市部純利潤最大(純利潤指的是收入總價款扣除成本及營業員工資后的余額,其它開支不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展,據調查,某家快遞公司,今年三月份與五月份完成投遞的快件總件數分別是5萬件和![]() 萬件,現假定該公司每月投遞的快件總件數的增長率相同.
萬件,現假定該公司每月投遞的快件總件數的增長率相同.
![]() 求該公司投遞快件總件數的月平均增長率;
求該公司投遞快件總件數的月平均增長率;
![]() 如果平均每人每月可投遞快遞
如果平均每人每月可投遞快遞![]() 萬件,那么該公司現有的16名快遞投遞員能否完成今年6月份的快遞投遞任務?
萬件,那么該公司現有的16名快遞投遞員能否完成今年6月份的快遞投遞任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
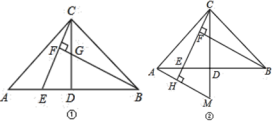
【題目】已知:在△ABC中,AC=BC,∠ACB=90°,點D是AB的中點,點E是AB邊上一點.
(1)直線BF垂直直線CE于點F,交CD于點G(如圖①),求證:AE=CG;
(2)直線AH垂直于直線CE,垂足為點H,交CD的延長線于點M(如圖②),找出圖中與BE相等的線段,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+b的圖象過P(1,4),Q(4,1)兩點,且與x軸交于A點.
(1)求此一次函數的解析式;
(2)求△POQ的面積;
(3)已知點M在x軸上,若使MP+MQ的值最小,
求點M的坐標及MP+MQ的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足為F.
(1)求證:△ABC≌△ADE;(圖1)
(2)求∠FAE的度數;(圖1)
(3)如圖2,延長CF到G點,使BF=GF,連接AG.求證:CD=CG;并猜想CD與2BF+DE的關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校參加區教育局舉辦的學生英語口語競賽,兩校參賽人數相等.比賽結束后,發現學生成績分別為7分、8分、9分、10分(滿分為10分).依據統計數據繪制了如下尚不完整的統計圖表. 

(1)在圖1中,“7分”所在扇形的圓心角等于°.
(2)請你將圖2的統計圖補充完整;
(3)經計算,乙校的平均分是8.3分,中位數是8分,請寫出甲校的平均分、中位數;并從平均分和中位數的角度分析哪個學校成績較好.
(4)如果該教育局要組織8人的代表隊參加市級團體賽,為便于管理,決定從這兩所學校中的一所挑選參賽選手,請你分析,應選哪所學校?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com