Question

求下面圖形的面積．（單位：cm）

Answer 1

考點：組合圖形的面積

專題：平面圖形的認識與計算

分析：，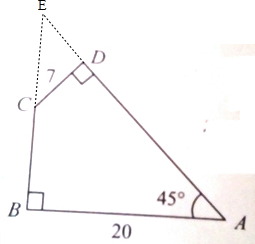
如圖，延長AD、BC相交于點E，因為∠DAB=45°，所以BE=AB=20（cm），∠CED=45°，所以DE=CD=7（cm）；然后根據直角三角形的面積公式，分別求出三角形ABE和三角形CDE的面積，再用三角形ABE的面積減去三角形CDE的面積，求出四邊形ABCD的面積是多少即可．

解答： 解：，
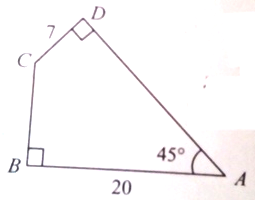
如圖，延長AD、BC相交于點E，因為∠DAB=45°，
所以BE=AB=20cm，∠CED=45°，所以DE=CD=7cm；
因此四邊形ABCD的面積是：
20×20÷2-7×7÷2
=400÷2-49÷2
=200-24.5
=175.5（cm²）
答：四邊形ABCD的面積是175.5cm²．

點評：此題主要考查了組合圖形的面積的求法，解答此題的關鍵是熟練掌握三角形的面積公式．