
題目列表(包括答案和解析)
(本小題滿分12分)
在一次奧運(yùn)知識有獎問答競賽中,甲、乙、丙同時(shí)回答一道有關(guān)奧運(yùn)知識的問題,已知甲答對這道題目的概率是![]() ,甲、丙兩人都答錯的概率是
,甲、丙兩人都答錯的概率是![]() ,乙、丙兩人都答對的概率是
,乙、丙兩人都答對的概率是![]() .
.
(1)求乙、丙兩人各自答對這道題目的概率;
(2)求甲、乙、丙三人中至少有兩人答對這道題目的概率.
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
 ,甲、丙兩人都回答錯的概率是
,甲、丙兩人都回答錯的概率是 ,乙、丙兩人都回答對的概率是
,乙、丙兩人都回答對的概率是 .
.2010年11月廣州成功舉辦了第十六屆亞運(yùn)會。在華南理工大學(xué)學(xué)生會舉行的亞運(yùn)知識有獎問答比賽中,甲、乙、丙同時(shí)回答一道有關(guān)亞運(yùn)知識的問題,已知甲回答對這道題目的概率是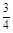 ,甲、丙兩人都回答錯的概率是
,甲、丙兩人都回答錯的概率是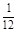 ,乙、丙兩人都回答對的概率是
,乙、丙兩人都回答對的概率是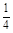 .
.
(1)求乙、丙兩人各自回答對這道題目的概率.
(2)(理)求回答對這道題目的人數(shù)的隨機(jī)變量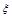 的分布列和期望.
的分布列和期望.
【解析】本試題主要考查了獨(dú)立事件概率的乘法計(jì)算公式的運(yùn)用。以及對立事件的概率的運(yùn)用。
(1)求乙、丙兩人各自回答對這道題的概率;
(2)求回答對該題的人數(shù)ξ的分布列和Eξ.
一、
1.C 2.C 3.C 4.D 5.C 6.B 7.C 8.A 9.D 10.C 
11.B 12.B
【解析】
11.提示:設(shè)曲線 在點(diǎn)
在點(diǎn) 處切線傾斜角為
處切線傾斜角為 ,則
,則 ,由
,由 ,得
,得 ,故
,故 ,所以
,所以 ,故選B.
,故選B.
12.提示:整形結(jié)合.
二、
13. 14.
14. 15.3 16.①③
15.3 16.①③
三、
17.解:(1)


 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為
(2)




18.(1)設(shè)乙、丙各自回答對的概率分別是 、
、 ,根據(jù)題意得:
,根據(jù)題意得:
 ,解得
,解得
(2) .
.
19.解:(1) 的解集有且只有一個(gè)元素
的解集有且只有一個(gè)元素
 或
或
又由 得
得
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí),

(2) ①
①
 ②
②
由式①-或②得
 .
.
20.解法一:

(1)設(shè) 交
交 于點(diǎn)
于點(diǎn)
 平面
平面 .
.
作 于點(diǎn)
于點(diǎn) ,連接
,連接 ,則由三垂線定理知:
,則由三垂線定理知: 是二面角
是二面角 的平面角.
的平面角.
由已知得 ,
,
 ,
,
∴二面角 的大小的60°.
的大小的60°.
(2)當(dāng) 是
是 中點(diǎn)時(shí),有
中點(diǎn)時(shí),有 平面
平面 .
.
證明:取 的中點(diǎn)
的中點(diǎn) ,連接
,連接 、
、 ,則
,則 ,
,
 ,故平面
,故平面 即平面
即平面 .
.
 又
又 平面
平面 ,
,
 平面
平面 .
.
解法二:由已知條件,以 為原點(diǎn),以
為原點(diǎn),以 、
、 、
、 為
為 軸、
軸、 軸、
軸、 軸建立空間直角坐標(biāo)系,則
軸建立空間直角坐標(biāo)系,則

(1) ,
,
 ,設(shè)平面
,設(shè)平面 的一個(gè)法向量為
的一個(gè)法向量為 ,
,
則 取
取
設(shè)平面 的一個(gè)法向量為
的一個(gè)法向量為 ,則
,則 取
取 .
.
 二面角
二面角 的大小為60°.
的大小為60°.
(2)令 ,則
,則 ,
,
 ,
,
由已知, ,要使
,要使 平面
平面 ,只需
,只需 ,即
,即
則有 ,得
,得 當(dāng)
當(dāng) 是
是 中點(diǎn)時(shí),有
中點(diǎn)時(shí),有 平面
平面 .
.
21.解:(1)① 當(dāng)直線 垂直于
垂直于 軸時(shí),則此時(shí)直線方程為
軸時(shí),則此時(shí)直線方程為 ,
,
 與圓的兩個(gè)交點(diǎn)坐標(biāo)為
與圓的兩個(gè)交點(diǎn)坐標(biāo)為 和
和 ,其距離為
,其距離為 ,滿足題意.
,滿足題意.
② 若直線 不垂直于
不垂直于 軸,設(shè)其方程
軸,設(shè)其方程 ,即
,即
設(shè)圓心到此直線的距離為 ,則
,則 ,得
,得
 ,
,
此時(shí)所求直線方程為
綜上所述,所求直線為 或
或 .
.
(2)設(shè)點(diǎn) 的坐標(biāo)為
的坐標(biāo)為 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為 ,則
,則 點(diǎn)坐標(biāo)是
點(diǎn)坐標(biāo)是

即
又 由已知,直線
由已知,直線 軸,所以,
軸,所以, ,
,
 點(diǎn)的軌跡議程是
點(diǎn)的軌跡議程是 ,
,
軌跡是焦點(diǎn)坐標(biāo)為 ,長軸為8的橢圓,并去掉
,長軸為8的橢圓,并去掉 兩點(diǎn).
兩點(diǎn).
22.解: ,
,
(1)由題意: 解得
解得 .
.
(2)方程 的叛別式
的叛別式 ,
,
① 當(dāng) ,即
,即 時(shí),
時(shí), ,
, 在
在 內(nèi)恒成立,此時(shí)
內(nèi)恒成立,此時(shí) 在
在 為增函數(shù);
為增函數(shù);
② 當(dāng) ,即
,即 或
或 時(shí),
時(shí),
要使 在
在 內(nèi)為增函數(shù),只需在
內(nèi)為增函數(shù),只需在 內(nèi)有
內(nèi)有 即可,
即可,
設(shè) ,
,
由 得
得 ,所以
,所以 .
.
由①②可知,若 在
在 內(nèi)為增函數(shù),則
內(nèi)為增函數(shù),則 的取值范圍是
的取值范圍是 .
.
www.ks5u.com
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com