
題目列表(包括答案和解析)
已知函數(shù)![]() ,項數(shù)為27的等差數(shù)列
,項數(shù)為27的等差數(shù)列![]() 滿足
滿足![]() ,且公差
,且公差![]() ≠0.若
≠0.若![]()
![]() =0,則當
=0,則當![]() =_____時,
=_____時,![]() =0.
=0.
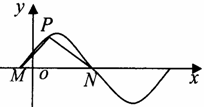 如圖所示,M,N是函數(shù)y=2sin(wx+
如圖所示,M,N是函數(shù)y=2sin(wx+![]() )(ω>0)圖像與x軸的交點,點P在M,N
)(ω>0)圖像與x軸的交點,點P在M,N
之間的圖像上運動,當△MPN面積最大時![]() ·
·![]() =0,則ω= ( )
=0,則ω= ( )
A.![]() B.
B.![]()
C.![]() D.8
D.8
(09年湖北鄂州5月模擬理)已知兩定點A(-3,0),B(3,0),動圓M與直線AB相切于點N,且![]() ,現(xiàn)分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
,現(xiàn)分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
⑴求動點P的軌跡方程;
⑵若直線xmy3=0截動點P的軌跡所得的弦長為5,求m的值;
⑶設過軌跡上的點P的直線與兩直線(09年山東省實驗中學綜合測試文)(13分)
直線y=kx+b與曲線![]() 交于A、B兩點,記△AOB的面積為S(O是坐
交于A、B兩點,記△AOB的面積為S(O是坐
標原點).
(1)求曲線的離心率;
(2)求在k=0,0<b<1的條件下,S的最大值;
(3)當|AB|=2,S=1時,求直線AB的方程.

以下四個命題,其中正確的是________.
①從勻速傳遞的產(chǎn)品生產(chǎn)流水線上,質(zhì)檢員每20分鐘從中抽取一件產(chǎn)品進行某項指標檢測,這樣的抽樣是分層抽樣;
②兩個隨機變量相關性越強,則相關系數(shù)的絕對值越接近于1;
③在回歸直線方程 =0.2x+12中,當解釋變量x每增加一個單位時,預報變量
=0.2x+12中,當解釋變量x每增加一個單位時,預報變量 平均增加0.2個單位;
平均增加0.2個單位;
④對分類變量X與Y,它們的隨機變量K2(χ2)的觀測值k來說,k越小,“X與Y有關系”的把握程度越大.
一 、選擇題
1.C. 2.A. 3.A. 4.A. 5.A. 6.C. 7.A. 8.A. 9.C. 10.D. 11.C.12.D.
一、 填空題
13. . 14.2. 15.16. 16.13.
. 14.2. 15.16. 16.13.
三、解答題
17.(理科) (1)由(1+tanA)(1+tanB)=2,得
tanA+tanB=1-tanAtanB,
即tan(A+B)=1.
∵A、B為△ABC內(nèi)角, ∴A+B= . 則 C=
. 則 C= (定值).
(定值).
(2)已知△ABC內(nèi)接于單位圓, ∴△ABC外接圓半徑R=1.
∴由正弦定理得: ,
, ,
, .
.
則△ABC面積S= =
= =
=
= =
=
= =
= .
.
∵ 0<B< , ∴
, ∴ .
.
故 當 時,△ABC面積S的最大值為
時,△ABC面積S的最大值為 .
.
(文科) (1) ,
,
 ,
, ,
, ,∴
,∴  .
.
∴ 向量 和
和 的夾角
的夾角 的大小為
的大小為 .
.
(2) .
.
以 和
和 為鄰邊的平行四邊形的面積
為鄰邊的平行四邊形的面積 ,
,
據(jù)此猜想, 的幾何意義是以
的幾何意義是以 、
、 為鄰邊的平行四邊形的面積.
為鄰邊的平行四邊形的面積.
18. (1)學生甲恰好抽到3道歷史題,2道地理題的概率為
 .
.
(2)若學生甲被評為良好,則他應答對5道題或4道題
而答對4道題包括兩種情況:①答對3道歷史題和1道地理(錯一道地理題);②答對2道歷史題和2道地理題(錯一道歷史題)。
設答對5道記作事件A;
答對3道歷史題,1道地理題記作事件B;
答對2道歷史題,2道地理題,記作事件C;
 ,
,
 ,
,
 .
.
∴甲被評為良好的概率為:
 .
.
19. (1)延長AC到G,使CG=AC,連結(jié)BG、DG,E是AB中點, .
.
故直線BG和BD所成的銳角(或直角)就是CE和BD所成的角.

(2)設C到平面ABD的距離為h


20. (1) .
.
(2) 由(1)知: ,故
,故 在
在 是增函數(shù).
是增函數(shù).
又 對于一切
對于一切 恒成立.
恒成立.
由定理知:存在
由(1)知: 

由 的一般性知:
的一般性知: .
.
21. (1)以 中點
中點 為原點,
為原點, 所在直線為
所在直線為 軸,建立平面直角坐標系,則
軸,建立平面直角坐標系,則 .
.
 |
設 ,由
,由 得
得 ,此即點
,此即點 的軌跡方程.
的軌跡方程.
(2)將 向右平移一個單位,再向下平移一個單位后,得到圓
向右平移一個單位,再向下平移一個單位后,得到圓 ,
,
依題意有 .
.
(3)不妨設點 在
在 的上方,并設
的上方,并設 ,則
,則 ,
,
所以 ,由于
,由于 且
且 ,
,
故 .
.
22.(理科)⑴ ∵f(x)+g(x)=ax,∴f(-x)+ g(-x)=a-x.
∵f(x)是奇函數(shù),g(x)是偶函數(shù),∴-f(x)+g(x)=a-x .
∴f(x)= ,g(x)=
,g(x)= .
.
⑵
 是R上的減函數(shù),
是R上的減函數(shù),
∴y=f -1(x)也是R上的減函數(shù).
又

⑶



 n>2,
n>2, 當
當 上是增函數(shù).
上是增函數(shù). 是減函數(shù);
是減函數(shù);
 上是減函數(shù).
上是減函數(shù). 是增函數(shù).
是增函數(shù).
(文科) (1)∵函數(shù) 在
在 和
和 時取得極值,∴-1,3是方程
時取得極值,∴-1,3是方程 的兩根,
的兩根,
∴
(2) ,當x變化時,有下表
,當x變化時,有下表
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f’(x)
+
0
-
0
+
f(x)
ㄊ
Max
c+5
ㄋ
Min
c-27
ㄊ
而 時f(x)的最大值為c+54.
時f(x)的最大值為c+54.
要使f(x)<2|c|恒成立,只要c+54<2|c|即可.
當c≥0時c+54<
當c<0時c+54<-
∴c∈(-∞,-18)∪(54,+∞).
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com