
已知等差數(shù)列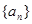 的公差不為零,其前n項和為
的公差不為零,其前n項和為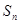 ,若
,若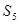 =70,且
=70,且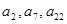 成等比數(shù)列,
成等比數(shù)列,
(1)求數(shù)列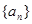 的通項公式;
的通項公式;
(2)設數(shù)列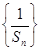 的前n項和為
的前n項和為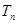 ,求證:
,求證: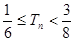 .
.
(1) ;(2)答案詳見解析.
;(2)答案詳見解析.
解析試題分析:數(shù)列問題要注意以下兩點①等差(比)數(shù)列中各有5個基本量,建立方程組可“知三求二”;②數(shù)列的本質(zhì)是定義域為正整數(shù)集或其有限子集的函數(shù),數(shù)列的通項公式即為相應的解析式,因此在解決數(shù)列問題時,應注意用函數(shù)的思想求解.(1)由題知,展開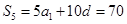 ,又
,又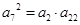 ,利用等差數(shù)列通項公式展開,得
,利用等差數(shù)列通項公式展開,得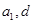 方程,聯(lián)立求
方程,聯(lián)立求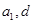 ,進而求數(shù)列
,進而求數(shù)列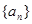 的通項公式;(2)求數(shù)列前
的通項公式;(2)求數(shù)列前 項和,首先考慮其通項公式
項和,首先考慮其通項公式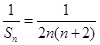 ,利用裂項相消法,求得
,利用裂項相消法,求得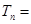
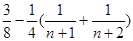 ,將其看作自變量為
,將其看作自變量為 的函數(shù),求其值域即可.
的函數(shù),求其值域即可.
試題解析:(1)由題知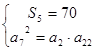 ,即
,即 , 2分
, 2分
解得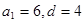 或
或 (舍去), 4分
(舍去), 4分
所以數(shù)列的通項公式為 . 4分
. 4分
(2)由(1)得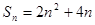 7分
7分
則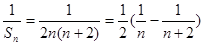 8分
8分
則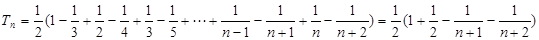
=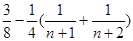 10分
10分
由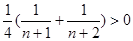 可知
可知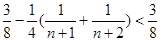 ,即
,即 11分
11分
由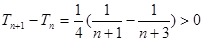 可知
可知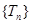 是遞增數(shù)列,則
是遞增數(shù)列,則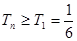 13分
13分
可證得: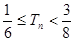 14分
14分
考點:1、等差數(shù)列的通項公式;2、等差數(shù)列前前 項和;3、裂項相消法.
項和;3、裂項相消法.


科目:高中數(shù)學 來源: 題型:解答題
設 是首項為a,公差為d的等差數(shù)列
是首項為a,公差為d的等差數(shù)列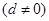 ,
, 是其前n項的和。記
是其前n項的和。記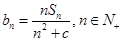 ,其中c為實數(shù)。
,其中c為實數(shù)。
(1)若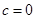 ,且
,且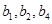 成等比數(shù)列,證明:
成等比數(shù)列,證明: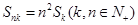 ;
;
(2)若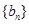 是等差數(shù)列,證明:
是等差數(shù)列,證明: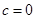 。
。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
從數(shù)列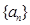 中抽出一些項,依原來的順序組成的新數(shù)列叫數(shù)列
中抽出一些項,依原來的順序組成的新數(shù)列叫數(shù)列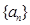 的一個子列.
的一個子列.
(1)寫出數(shù)列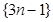 的一個是等比數(shù)列的子列;
的一個是等比數(shù)列的子列;
(2)設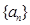 是無窮等比數(shù)列,首項
是無窮等比數(shù)列,首項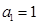 ,公比為
,公比為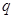 .求證:當
.求證:當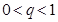 時,數(shù)列
時,數(shù)列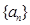 不存在
不存在
是無窮等差數(shù)列的子列.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
在數(shù)列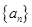 中,
中,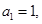 且對任意的
且對任意的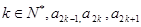 成等比數(shù)列,其公比為
成等比數(shù)列,其公比為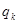 ,
,
(1)若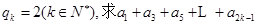 ;
;
(2)若對任意的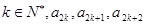 成等差數(shù)列,其公差為
成等差數(shù)列,其公差為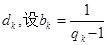 .
.
①求證: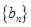 成等差數(shù)列,并指出其公差;
成等差數(shù)列,并指出其公差;
②若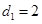 ,試求數(shù)列
,試求數(shù)列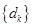 的前
的前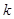 項和
項和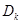 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知數(shù)列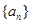 是公差不為0的等差數(shù)列,
是公差不為0的等差數(shù)列,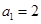 ,且
,且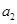 ,
,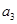 ,
,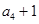 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設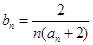 ,求數(shù)列
,求數(shù)列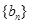 的前
的前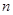 項和
項和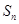 。
。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設各項均為正數(shù)的數(shù)列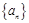 的前n項和為Sn,已知
的前n項和為Sn,已知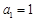 ,且
,且 對一切
對一切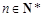 都成立.
都成立.
(1)若λ = 1,求數(shù)列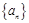 的通項公式;
的通項公式;
(2)求λ的值,使數(shù)列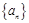 是等差數(shù)列.
是等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知數(shù)列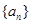 是公差不為0的等差數(shù)列,a1=2且a2,a3,a4+1成等比數(shù)列。
是公差不為0的等差數(shù)列,a1=2且a2,a3,a4+1成等比數(shù)列。
(1)求數(shù)列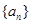 的通項公式;
的通項公式;
(2)設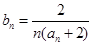 ,求數(shù)列
,求數(shù)列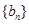 的前
的前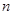 項和
項和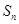
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
知{an}是首項為-2的等比數(shù)列,Sn是其前n項和,且S3,S2,S4成等差數(shù)列,
(1)求數(shù)列{an}的通項公式.
(2)若bn=log2|an|,求數(shù)列{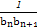 }的前n項和Tn.
}的前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知等差數(shù)列{an}是遞增數(shù)列,且滿足a4·a7=15,a3+a8=8.
(1)求數(shù)列{an}的通項公式;
(2)令bn= (n≥2),b1=
(n≥2),b1=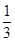 ,求數(shù)列{bn}的前n項和Sn.
,求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com