
【題目】在三棱錐![]() 中,
中,![]() ,平面
,平面![]() 和平面
和平面![]() 所成角為
所成角為![]() ,則三棱錐
,則三棱錐![]() 外接球的體積為( )
外接球的體積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
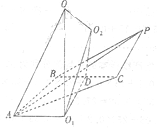
【解析】分析:先明確球心的位置:過(guò)△ABC的外心![]() 作平面ABC的垂線,過(guò)△PBC的外心
作平面ABC的垂線,過(guò)△PBC的外心![]() 作平面PBC的垂線,設(shè)兩條垂線交于點(diǎn)O,則O為三棱錐
作平面PBC的垂線,設(shè)兩條垂線交于點(diǎn)O,則O為三棱錐![]() 外接球的球心,然后把問(wèn)題轉(zhuǎn)化為解三角形的問(wèn)題.
外接球的球心,然后把問(wèn)題轉(zhuǎn)化為解三角形的問(wèn)題.
詳解:如圖,過(guò)△ABC的外心![]() 作平面ABC的垂線,過(guò)△PBC的外心
作平面ABC的垂線,過(guò)△PBC的外心![]() 作平面PBC的垂線,設(shè)兩條垂線交于點(diǎn)O,則O為三棱錐
作平面PBC的垂線,設(shè)兩條垂線交于點(diǎn)O,則O為三棱錐![]() 外接球的球心,過(guò)點(diǎn)
外接球的球心,過(guò)點(diǎn)![]() 作
作![]() ,連接
,連接![]() ,則BC⊥平面
,則BC⊥平面![]() ,BC⊥平面
,BC⊥平面![]() ,所以
,所以![]() 四點(diǎn)共面,所以BC⊥
四點(diǎn)共面,所以BC⊥![]() ,
,
由BC⊥![]() ,BC⊥
,BC⊥![]() ,所以∠
,所以∠![]() 為平面PBC和平面ABC所成角,即∠
為平面PBC和平面ABC所成角,即∠![]() ,
,
由![]() ,得
,得![]() ,由余弦定理得
,由余弦定理得![]() ,
,
由正弦定理得![]() ,即
,即![]() ,又因?yàn)?/span>
,又因?yàn)?/span>![]() ,所以由余弦定理得
,所以由余弦定理得![]() ,所以
,所以![]() ,所以
,所以![]() ,三棱錐
,三棱錐![]() 外接球的體積為
外接球的體積為![]()
故選:A


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)在第![]() 年年初購(gòu)買(mǎi)一臺(tái)價(jià)值為
年年初購(gòu)買(mǎi)一臺(tái)價(jià)值為![]() 萬(wàn)元的設(shè)備
萬(wàn)元的設(shè)備![]() ,
,![]() 的價(jià)值在使用過(guò)程中逐年減少?gòu)牡?/span>
的價(jià)值在使用過(guò)程中逐年減少?gòu)牡?/span>![]() 年到第
年到第![]() 年,每年年初
年,每年年初![]() 的價(jià)值比上年年初減少
的價(jià)值比上年年初減少![]() 萬(wàn)元;從第
萬(wàn)元;從第![]() 年開(kāi)始,每年年初
年開(kāi)始,每年年初![]() 的價(jià)值為上年年初的
的價(jià)值為上年年初的![]() .
.
(1)求第![]() 年年初
年年初![]() 的價(jià)值
的價(jià)值![]() 的表達(dá)式.
的表達(dá)式.
(2)設(shè)![]() ,若
,若![]() 大于
大于![]() 萬(wàn),則
萬(wàn),則![]() 繼續(xù)使用;否則,必須在第
繼續(xù)使用;否則,必須在第![]() 年年初對(duì)
年年初對(duì)![]() 更新.
更新.
①求![]() ;
;
②證明:必須在第![]() 年年初對(duì)
年年初對(duì)![]() 更新.(若
更新.(若![]() 是遞減數(shù)列,
是遞減數(shù)列,![]() 也是遞減數(shù)列).
也是遞減數(shù)列).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“微信運(yùn)動(dòng)”是手機(jī)![]() 推出的多款健康運(yùn)動(dòng)軟件中的一款,楊老師的微信朋友圈內(nèi)有
推出的多款健康運(yùn)動(dòng)軟件中的一款,楊老師的微信朋友圈內(nèi)有![]() 位好友參與了“微信運(yùn)動(dòng)”,他隨機(jī)選取了
位好友參與了“微信運(yùn)動(dòng)”,他隨機(jī)選取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),統(tǒng)計(jì)其在某一天的走路步數(shù).其中,女性好友的走路步數(shù)數(shù)據(jù)記錄如下:
人),統(tǒng)計(jì)其在某一天的走路步數(shù).其中,女性好友的走路步數(shù)數(shù)據(jù)記錄如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步數(shù)情況可分為五個(gè)類(lèi)別: ![]() 步)(說(shuō)明:“
步)(說(shuō)明:“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() .下同),
.下同), ![]() 步),
步), ![]() 步),
步), ![]() 步),
步), ![]() 步及以
步及以![]() ),且
),且![]() 三種類(lèi)別人數(shù)比例為
三種類(lèi)別人數(shù)比例為![]() ,將統(tǒng)計(jì)結(jié)果繪制如圖所示的條形圖.
,將統(tǒng)計(jì)結(jié)果繪制如圖所示的條形圖.

若某人一天的走路步數(shù)超過(guò)![]() 步被系統(tǒng)認(rèn)定為“衛(wèi)健型",否則被系統(tǒng)認(rèn)定為“進(jìn)步型”.
步被系統(tǒng)認(rèn)定為“衛(wèi)健型",否則被系統(tǒng)認(rèn)定為“進(jìn)步型”.
(1)若以楊老師選取的好友當(dāng)天行走步數(shù)的頻率分布來(lái)估計(jì)所有微信好友每日走路步數(shù)的概率分布,請(qǐng)估計(jì)楊老師的微信好友圈里參與“微信運(yùn)動(dòng)”的![]() 名好友中,每天走路步數(shù)在
名好友中,每天走路步數(shù)在![]() 步的人數(shù);
步的人數(shù);
(2)請(qǐng)根據(jù)選取的樣本數(shù)據(jù)完成下面的![]() 列聯(lián)表并據(jù)此判斷能否有
列聯(lián)表并據(jù)此判斷能否有![]() 以上的把握認(rèn)定“認(rèn)定類(lèi)型”與“性別”有關(guān)?
以上的把握認(rèn)定“認(rèn)定類(lèi)型”與“性別”有關(guān)?
衛(wèi)健型 | 進(jìn)步型 | 總計(jì) | |
男 | 20 | ||
女 | 20 | ||
總計(jì) | 40 |
(3)若從楊老師當(dāng)天選取的步數(shù)大于10000的好友中按男女比例分層選取![]() 人進(jìn)行身體狀況調(diào)查,然后再?gòu)倪@
人進(jìn)行身體狀況調(diào)查,然后再?gòu)倪@![]() 位好友中選取
位好友中選取![]() 人進(jìn)行訪談,求至少有一位女性好友的概率.
人進(jìn)行訪談,求至少有一位女性好友的概率.
附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知平面上動(dòng)點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離與到直線
的距離與到直線![]() 的距離之比為
的距離之比為![]() ,記動(dòng)點(diǎn)
,記動(dòng)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設(shè)![]() 是曲線
是曲線![]() 上的動(dòng)點(diǎn),直線
上的動(dòng)點(diǎn),直線![]() 的方程為
的方程為![]() .
.
①設(shè)直線![]() 與圓
與圓![]() 交于不同兩點(diǎn)
交于不同兩點(diǎn)![]() ,
, ![]() ,求
,求![]() 的取值范圍;
的取值范圍;
②求與動(dòng)直線![]() 恒相切的定橢圓
恒相切的定橢圓![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲線
是曲線![]() :
: ![]() 上的動(dòng)點(diǎn),是否存在直線
上的動(dòng)點(diǎn),是否存在直線![]() :
: ![]() 恒相切的定曲線
恒相切的定曲線![]() ?若存在,直接寫(xiě)出曲線
?若存在,直接寫(xiě)出曲線![]() 的方程;若不存在,說(shuō)明理由.
的方程;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
(1)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線為
處的切線為![]() ,
, ![]() 與
與![]() 軸的交點(diǎn)坐標(biāo)為
軸的交點(diǎn)坐標(biāo)為![]() ,求
,求![]() 的值;
的值;
(2)討論![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
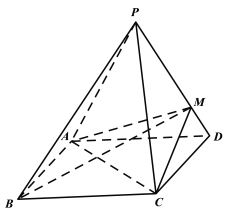
【題目】如圖,四棱錐P-ABCD的底面是矩形,側(cè)面PAD為等邊三角形,AB=![]() ,AD=
,AD=![]() , PB=
, PB=![]() .
.
(1)求證:平面PAD⊥平面ABCD;
(2)M是棱PD上一點(diǎn),三棱錐M-ABC的體積為1.記三棱錐P-MAC的體積為![]() ,三棱錐M-ACD的體積為
,三棱錐M-ACD的體積為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】據(jù)統(tǒng)計(jì),在不考慮其他因素的條件下,某段下水道的排水量V(單位:立方米/小時(shí))是垃圾雜物密度x(單位:千克/立方米)的函數(shù)。當(dāng)下水道的垃圾雜物密度達(dá)到3千克/立方米時(shí),會(huì)造成堵塞,此時(shí)排水量為0;當(dāng)垃圾雜物密度不超過(guò)0.5千克/立方米時(shí),排水量是80立方米/小時(shí)。研究表明,當(dāng)![]() 時(shí),排水量V是垃圾雜物密度x的一次函數(shù).
時(shí),排水量V是垃圾雜物密度x的一次函數(shù).
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的解析式;
的解析式;
(2)當(dāng)垃圾雜物密度x為多大時(shí),垃圾雜物量(單位時(shí)間內(nèi)通過(guò)某段下水道的垃圾雜物量,單位:千克/小時(shí))![]() 可以達(dá)到最大?求出這個(gè)最大值.
可以達(dá)到最大?求出這個(gè)最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某高校在2017年的自主招生考試成績(jī)中隨機(jī)抽取100名學(xué)生的筆試成績(jī),按成績(jī)分組,得到的頻率分布表如下:
組號(hào) | 分組 | 頻率 |
第1組 | [160,165) | 0.05 |
第2組 | [165,170) | 0.35 |
第3組 | [170,175) | ① |
第4組 | [175,180) | 0.20 |
第5組 | [180,185] | 0.10 |
(1)請(qǐng)先求出頻率分布表中①處應(yīng)填寫(xiě)的數(shù)據(jù),并完成如圖所示的頻率分布直方圖;
(2)為了能選拔出最優(yōu)秀的學(xué)生,高校決定在筆試成績(jī)高的第3,4,5組中用分層抽樣的方法抽取6名學(xué)生進(jìn)入第二輪面試,求第3,4,5組每組各應(yīng)抽取多少名學(xué)生進(jìn)入第二輪面試.
(3)根據(jù)直方圖估計(jì)這次自主招生考試筆試成績(jī)的平均數(shù)和中位數(shù);

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】青島二中有羽毛球社乒乓球社和籃球社,三個(gè)社團(tuán)的人數(shù)分別為27,9,18,現(xiàn)采用分層抽樣的方法從這三個(gè)社團(tuán)中抽取6人參加活動(dòng).
(1)求應(yīng)從這三個(gè)社團(tuán)中分別抽取的學(xué)生人數(shù);
(2)將抽取的6名學(xué)生進(jìn)行編號(hào),編號(hào)分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,從這6名學(xué)生中隨機(jī)抽出2名參加體育測(cè)試.
,從這6名學(xué)生中隨機(jī)抽出2名參加體育測(cè)試.
①用所給的編號(hào)列出所有可能的結(jié)果;
②設(shè)事件![]() 是“編號(hào)為
是“編號(hào)為![]() ,
,![]() 的兩名學(xué)生至少有一人被抽到”,求事件
的兩名學(xué)生至少有一人被抽到”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com