若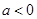
時，函數
在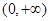
上有且只有一個零點，則
=
閱讀快車系列答案科目：高中數學 來源： 題型：
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
查看答案和解析>>
科目：高中數學 來源： 題型：
(本小題滿分16分)
探究函數
,x∈(0,+∞)的最小值，并確定相應的x的值，列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
請觀察表中y值隨x值變化的特點，完成下列問題：
(1)若函數,(x>0)在區間(0,2)上遞減，則在 上遞增；
(2)當x= 時，,(x>0)的最小值為 ；
(3)試用定義證明,(x>0)在區間(0,2)上遞減；
(4)函數
,(a>0, 且a≠1）有最值嗎？是最大值還是最小值？此時x為何值？（只寫結果，不要求寫過程）.
查看答案和解析>>
科目：高中數學 來源： 題型：
(本小題滿分16分)
探究函數
,x∈(0,+∞)的最小值，并確定相應的x的值，列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
請觀察表中y值隨x值變化的特點，完成下列問題：
(1)若函數,(x>0)在區間(0,2)上遞減，則在 上遞增；
(2)當x= 時，,(x>0)的最小值為 ；
(3)試用定義證明,(x>0)在區間(0,2)上遞減；
(4)函數
,(a>0, 且a≠1）有最值嗎？是最大值還是最小值？此時x為何值？（只寫結果，不要求寫過程）.
查看答案和解析>>
科目：高中數學 來源： 題型：
(本小題滿分16分)
探究函數
,x∈(0,+∞)的最小值，并確定相應的x的值，列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
請觀察表中y值隨x值變化的特點，完成下列問題：
(1)若函數,(x>0)在區間(0,2)上遞減，則在 上遞增；
(2)當x= 時，,(x>0)的最小值為 ；
(3)試用定義證明,(x>0)在區間(0,2)上遞減；
(4)函數
,(a>0, 且a≠1）有最值嗎？是最大值還是最小值？此時x為何值？（只寫結果，不要求寫過程）.
查看答案和解析>>
科目：高中數學 來源：2011-2012學年四川省成都市模擬考試理科數學試卷（解析版） 題型：解答題
已知函數
其中
為自然對數的底數，
.(Ⅰ)設
，求函數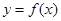
的最值；（Ⅱ）若對于任意的
，都有
成立，求
的取值范圍.
【解析】第一問中，當
時，
，
．結合表格和導數的知識判定單調性和極值，進而得到最值。
第二問中，∵
，
，
∴原不等式等價于：
,
即
, 亦即
分離參數的思想求解參數的范圍
解：（Ⅰ)當時，，．
當在
上變化時，
，
的變化情況如下表：
|
|
|
|
|
|
|
|
|
|
－ |
|
＋ |
|
|
|
|
|
|
|
1／e |
∴
時，
，
．
(Ⅱ)∵，，
∴原不等式等價于：
,
即, 亦即．
∴對于任意的
，原不等式恒成立,等價于對
恒成立,
∵對于任意的時, 
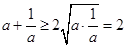（當且僅當
時取等號）．
∴只需
，即
，解之得
或
.
因此，的取值范圍是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，在
上有且只有一個零點，即
，而，
時，
，
，所以，
時，等式成立且只有一個解，注意到等號右邊函數式中的
，
，為使
，
=
