
已知函數 ,
,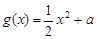 (
( 為常數),直線
為常數),直線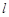 與函數
與函數 、
、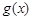 的圖象都相切,且
的圖象都相切,且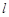 與函數
與函數 圖象的切點的橫坐標為
圖象的切點的橫坐標為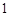 .
.
(1)求直線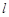 的方程及
的方程及 的值;
的值;
(2)若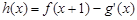 [注:
[注: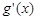 是
是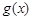 的導函數],求函數
的導函數],求函數 的單調遞增區間;
的單調遞增區間;
(3)當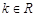 時,試討論方程
時,試討論方程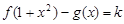 的解的個數.
的解的個數.
(1)  ;
;  ;(2)
;(2)  ,
,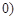 ;(3)詳見解析.
;(3)詳見解析.
解析試題分析:(1)利用函數在 處的導數,等于在
處的導數,等于在 處切線的斜率,所以先求
處切線的斜率,所以先求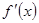 ,再求
,再求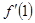 ,直線
,直線 的斜率就是
的斜率就是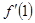 ,直線
,直線 過點
過點 ,代入得到直線
,代入得到直線 的方程,直線
的方程,直線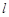 與
與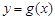 的圖象相切,所以代入聯立
的圖象相切,所以代入聯立 ,
, 得到
得到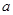 值;(2)先求
值;(2)先求 , 得到
, 得到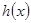 ,再求
,再求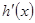 ,令
,令 ,得到
,得到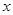 的取值范圍,即求得函數
的取值范圍,即求得函數 的單調遞增區間;(3)令
的單調遞增區間;(3)令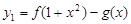
 ,
, ,再求
,再求 ,得到極值點,然后列表分析當
,得到極值點,然后列表分析當 變化時,
變化時, ,
, 的變化情況,結合
的變化情況,結合 為偶函數,畫出
為偶函數,畫出 的函數圖形,再畫
的函數圖形,再畫 ,當直線
,當直線 上下變化時,可以看出交點的變化,根據交點的不同,從而確定,再不同
上下變化時,可以看出交點的變化,根據交點的不同,從而確定,再不同 的范圍下得到不同的交點個數.此問注意分類討論思想的使用,不要遺漏情況.屬于較難習題.
的范圍下得到不同的交點個數.此問注意分類討論思想的使用,不要遺漏情況.屬于較難習題.
試題解析:(1)解:由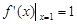 ,
,
故直線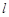 的斜率為
的斜率為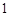 ,切點為
,切點為 ,
,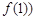 ,即
,即 ,
,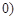 ,
,
所以直線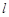 的方程為
的方程為 . 3分
. 3分
直線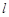 與
與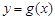 的圖象相切,等價于方程組
的圖象相切,等價于方程組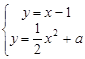 只有一解,
只有一解,
即方程 有兩個相等實根,
有兩個相等實根,
所以令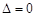 ,解得
,解得 . 5分
. 5分
(2)因為
 ,
,
由 ,
,
令 ,所以
,所以 ,
,
所以函數 的單調遞增區間是
的單調遞增區間是 ,
,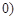 . 8分
. 8分
(3)令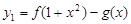
 ,
, ,
,
由 ,令
,令 ,得
,得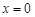 ,
, ,
,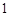 , 10分
, 10分
當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表: