
【題目】下列4個命題:
①“若![]() 成等比數(shù)列,則
成等比數(shù)列,則![]() ”的逆命題;
”的逆命題;
②“如果![]() ,則
,則![]() ”的否命題;
”的否命題;
③在![]() 中,“若
中,“若![]() ”則“
”則“![]() ”的逆否命題;
”的逆否命題;
④當![]() 時,若
時,若![]() 對
對![]() 恒成立,則
恒成立,則![]() 的取值范圍是
的取值范圍是![]() .
.
其中真命題的序號是__________.
【答案】②,③
【解析】①“若a、G、b成等比數(shù)列,則G2=ab”的逆命題為“若G2=ab,則a、G、b成等比數(shù)列”,
不正確,比如a=G=b=0,則a、G、b不成等比數(shù)列,故①錯;
②“如果x2+x60,則x>2”的否命題為“②“如果x2+x6<0,則x2”的否命題”,
由x2+x6<0,可得3<x<2,推得x2,故②對;
③在△ABC中,“若A>B”“a>b”“2RsinA>2RsinB”“sinA>sinB”(R為外接圓的半徑)則其逆否命題正確,故③對;
④當0απ時,若8x2(8sinα)x+cos2α0對x∈R恒成立,即有△=64sin2α32cos2α0,
即有12cos2α0,即為cos2α![]() ,可得
,可得![]() ,
,
解得![]() ,故④錯。
,故④錯。
故真命題的序號是②③。


科目:高中數(shù)學 來源: 題型:
【題目】4月23日是世界讀書日,惠州市某中學在此期間開展了一系列的讀書教育活動。為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調(diào)查。下面是根據(jù)調(diào)查結果繪制的學生日均課外閱讀時間(單位:分鐘)的頻率分布直方圖,且將日均課外閱讀時間不低于60分鐘的學生稱為“讀書迷”,低于60分鐘的學生稱為“非讀書迷”.
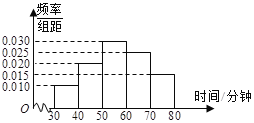
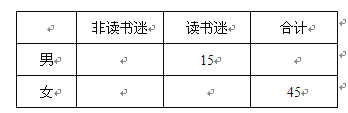
(Ⅰ)根據(jù)已知條件完成下面2×2列聯(lián)表,并據(jù)此判斷是否有99%的把握認為“讀書迷”與性別有關?
(Ⅱ)將頻率視為概率,現(xiàn)在從該校大量學生中用隨機抽樣的方法每次抽取1人,共抽取3次,記被抽取的3人中“讀書迷”的人數(shù)為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列、數(shù)學期望
的分布列、數(shù)學期望![]() 和方差
和方差![]() .
.
附: 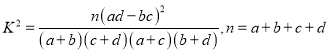
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 為線段
為線段![]() 上的一動點.
上的一動點.
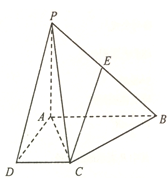
(Ⅰ)若![]() 為線段
為線段![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(Ⅱ)當直線![]() 與平面
與平面![]() 所成角小于
所成角小于![]() ,求
,求![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在某次水下科研考察活動中,需要潛水員潛入水深為60米的水底進行作業(yè),根據(jù)已往經(jīng)驗,潛水員下潛的平均速度為![]() (米/單位時間),每單位時間的用氧量為
(米/單位時間),每單位時間的用氧量為![]() (升),在水底作業(yè)10個單位時間,每單位時間用氧量為
(升),在水底作業(yè)10個單位時間,每單位時間用氧量為![]() (升),返回水面的平均速度為
(升),返回水面的平均速度為![]() (米/單位時間),每單位時間用氧量為
(米/單位時間),每單位時間用氧量為![]() (升),記該潛水員在此次考察活動中的總用氧量為
(升),記該潛水員在此次考察活動中的總用氧量為![]() (升).
(升).
(1)求![]() 關于
關于![]() 的函數(shù)關系式;
的函數(shù)關系式;
(2)若![]() ,求當下潛速度
,求當下潛速度![]() 取什么值時,總用氧量最少.
取什么值時,總用氧量最少.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,
, ![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程和離心率.
的方程和離心率.
(2)設點![]() ,動點
,動點![]() 在
在![]() 軸上,動點
軸上,動點![]() 在橢圓
在橢圓![]() 上,且點
上,且點![]() 在
在![]() 軸的右側.若
軸的右側.若![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知城![]() 和城
和城![]() 相距
相距![]() ,現(xiàn)計劃以
,現(xiàn)計劃以![]() 為直徑的半圓上選擇一點
為直徑的半圓上選擇一點![]() (不與點
(不與點![]() ,
, ![]() 重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城
重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為對城
的總影響度為對城![]() 與城
與城![]() 的影響度之和.記點到
的影響度之和.記點到![]() 城
城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理廠對城
處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() .統(tǒng)計調(diào)查表明:垃圾處理廠對城
.統(tǒng)計調(diào)查表明:垃圾處理廠對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數(shù)為4;對城
的距離的平方成反比例關系,比例系數(shù)為4;對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數(shù)為
的距離的平方成反比例關系,比例系數(shù)為![]() .當垃圾處理廠建在
.當垃圾處理廠建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065.
的總影響度為0.065.
(1)將![]() 表示成
表示成![]() 的函數(shù).
的函數(shù).
(2)討論(1)中函數(shù)的單調(diào)性,并判斷在![]() 上是否存在一點,使建在此處的垃圾處理廠對城
上是否存在一點,使建在此處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知兩條不重合的直線![]() 和兩個不重合的平面
和兩個不重合的平面![]() ,若
,若![]() ,則下列四個命題:①若
,則下列四個命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,則
,則![]() ; ③若
; ③若![]() ,則
,則![]() ;④若
;④若![]() ,則
,則![]() ,其中正確命題的個數(shù)是( )
,其中正確命題的個數(shù)是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系中,以坐標原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 為參數(shù)).
為參數(shù)).
(1)直線![]() 過
過![]() 且與曲線
且與曲線![]() 相切,求直線
相切,求直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 與點
與點![]() 關于
關于![]() 軸對稱,求曲線
軸對稱,求曲線![]() 上的點到點
上的點到點![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() 的極值;
的極值;
(2)若![]() ,是否存在
,是否存在![]() ,使
,使![]() 的極值大于零?若存在,求出
的極值大于零?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com