
���}Ŀ���O����(sh��)![]() ��
��![]() ������
������![]() ��e����Ȼ����(sh��)�ĵה�(sh��)��
��e����Ȼ����(sh��)�ĵה�(sh��)��
��1����![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c����a��ȡֵ������
�ϴ��ڃɂ��Oֵ�c����a��ȡֵ������
��2����![]() ���O
���O![]() ��
��![]() ����
����![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c
�ϴ��ڃɂ��Oֵ�c![]() ��
��![]() ����
����![]() �����C��
�����C�� ![]() ��
��
���𰸡���1��![]() ����2���C��Ҋ����.
����2���C��Ҋ����.
��������
��1��![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c���t
�ϴ��ڃɂ��Oֵ�c���t![]() �Ѓɸ����ٷ��x����(sh��)����������(sh��)�о����ɣ�
�Ѓɸ����ٷ��x����(sh��)����������(sh��)�о����ɣ�
��2��Ҫ�C![]() ���C
���C![]() ��
��![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c
�ϴ��ڃɂ��Oֵ�c![]() ��
��![]() ����
����![]() ����
����![]() �Ѓɂ����c
�Ѓɂ����c![]() ��
��![]() ���ɵ�
���ɵ�![]() ���O
���O![]() ���t
���t![]() ��
��![]() �����C
�����C![]() ��
��![]() ������
������![]() �r��
�r��![]() ���O����(sh��)
���O����(sh��)![]() ��
��![]() �����Ì���(sh��)������{�Լ�����(sh��)����ֵ�����ɵ��C.
�����Ì���(sh��)������{�Լ�����(sh��)����ֵ�����ɵ��C.
�⣺��1��![]() �����}���֪��
�����}���֪��![]() ��
��![]() ���Ѓɂ���ͬ�Č���(sh��)����
���Ѓɂ���ͬ�Č���(sh��)����
��![]() ��ֻ�躯��(sh��)
��ֻ�躯��(sh��)![]() ��
��![]() �D���Ѓɂ����c��
�D���Ѓɂ����c��
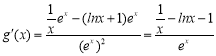 ����֪
����֪![]() ��
��![]() �Ϟ�p����(sh��)����
�Ϟ�p����(sh��)����![]() ��
��
��![]() �r��
�r��![]() ��
��![]() ��������(sh��)����
��������(sh��)����![]() �r��
�r��![]() ��
��![]() ��p����(sh��)��
��p����(sh��)��
����![]() ������
������![]() ���֮�
���֮�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
Ҫʹ![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c���t
�ϴ��ڃɂ��Oֵ�c���t![]() ��
��
��![]() ��ȡֵ������
��ȡֵ������![]() ��
��
��2��![]() ��
��![]() ��
��![]()
![]() ��
��![]() �ϴ��ڃɂ��Oֵ�c
�ϴ��ڃɂ��Oֵ�c![]() ��
��![]() ����
����![]()
![]() �Ѓɂ����c
�Ѓɂ����c![]() ��
��![]() ��
��
�t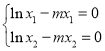 �����
�����![]()
����
��![]() ���O
���O![]() �t
�t![]() �����
�����![]() ��
��![]()
Ҫ�C![]() �����C
�����C![]() ��
��![]()
����![]() �r��
�r��![]() ���O����(sh��)
���O����(sh��)![]() ��
��![]() ���t
���t
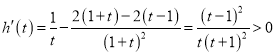
���ԣ�![]() ��
��![]() �ϵ�������(sh��)����
�ϵ�������(sh��)����![]() �����
�����![]()
���ǣ���![]() �r����
�r����![]() ��
��
���ԣ���![]() ��������
��������![]() �����C
�����C



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D����������ABCD��A1B1C1D1�У�O��BD�����c��E����CC1������һ�c��
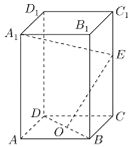
��1���C����BD��A1E��
��2�����AB=2��![]() ��OE��A1E����AA1���L��
��OE��A1E����AA1���L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����֪��헾�������(sh��)�Ĕ�(sh��)��![]() ��ǰ
��ǰ![]() 헺͞�
헺͞�![]() �ҝM��:
�ҝM��:![]()
(1)��(sh��)��![]() ��ͨ헹�ʽ��
��ͨ헹�ʽ��
(2)�O![]() ��
��![]() ��ֵ��
��ֵ��
(3)�Ƿ���ڴ���2��������(sh��)![]() ʹ��
ʹ��![]() ?������,������з��ϗl����
?������,������з��ϗl����![]() ��������,Ո�f������.
��������,Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�����
�У�����![]() �������Σ�
��������![]() ����
����![]() ��
��![]() ��
��![]() �龀��
�龀��![]() �����c����
�����c����![]() �龀��
�龀��![]() �ϵĄ��c������
�ϵĄ��c������![]() ��.
��.
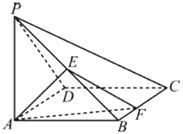
��1��ƽ��![]() �cƽ��
�cƽ��![]() �Ƿ��ഹֱ������ǣ�Ո�C����������ǣ�Ո�f�����ɣ�
�Ƿ��ഹֱ������ǣ�Ո�C����������ǣ�Ո�f�����ɣ�
��2��������![]() ������ֵ��ȡֵ����.
������ֵ��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����һ���L��![]() ������
������![]() �ľ����FƤ����D1��������һ��ֱ�LjA�Ώ��ܣ���D3�������ھ��ε����g��һ�l�����������������_�������õăɲ��ַքe�����w�e��ȵ�б�؈A�����D2����Ȼ������һ���m�����Dƴ�ӳ�ֱ�LjA�Ώ��ܣ���D3������Ӌƴ�ӓp�IJ��֣�����ʹ��ֱ�LjA�Ώ��ܵ��w�e���
�ľ����FƤ����D1��������һ��ֱ�LjA�Ώ��ܣ���D3�������ھ��ε����g��һ�l�����������������_�������õăɲ��ַքe�����w�e��ȵ�б�؈A�����D2����Ȼ������һ���m�����Dƴ�ӳ�ֱ�LjA�Ώ��ܣ���D3������Ӌƴ�ӓp�IJ��֣�����ʹ��ֱ�LjA�Ώ��ܵ��w�e���
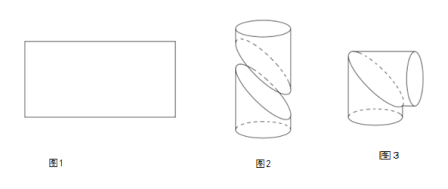
��1����ֱ�LjA�Ώ��ܣ��D3�����w�e��
��2����б����E�A�Ľ��ࣻ
��3���������ĈD1�н����m��?sh��)�����ϵ��ʹ�����������ķ��̞�![]() ��������̲��������D��
��������̲��������D��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D���������FP-ABCD�У�PD��ƽ��ABCD������ABCD�����Σ���BAD=60����AB=2��PD=![]() ��O��AC�cBD�Ľ��c��E����PB��һ�c��
��O��AC�cBD�Ľ��c��E����PB��һ�c��

��1���C����ƽ��EAC��ƽ��PBD��
��2����PD��ƽ��EAC���������FP-EAD���w�e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���������傀���}��
�ٺ���(sh��)![]() ����С��������
������������![]() ��
��
�ڽK߅��![]() �S�ϵĽǵļ�����
�S�ϵĽǵļ�����![]() ��
��
����ͬһ����ϵ�У�����(sh��)![]() �ĈD��ͺ���(sh��)
�ĈD��ͺ���(sh��)![]() �ĈD�������������c��
�ĈD�������������c��
�ܰѺ���(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ����λ�õ�
����λ�õ�![]() �ĈD��
�ĈD��
�ݺ���(sh��)![]() ��
��![]() ���ǜp����(sh��)��
���ǜp����(sh��)��
���������}����̖�ǣ�������
A.�٢ڢ�B.�٢�C.�ۢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���P�ں���(sh��)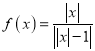 ���o�������Ă����}����1����
���o�����������}����1����![]() �r��
�r��![]() ���{�f�p�қ]����ֵ����2������
���{�f�p�қ]����ֵ����2������![]() һ���Ќ���(sh��)�⣻��3���������
һ���Ќ���(sh��)�⣻��3���������![]() ��
��![]() �鳣��(sh��)���н⣬�t��Â���(sh��)һ����ż��(sh��)����4��
�鳣��(sh��)���н⣬�t��Â���(sh��)һ����ż��(sh��)����4��![]() ��ż����(sh��)������Сֵ.���м����}����̖��____________.
��ż����(sh��)������Сֵ.���м����}����̖��____________.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���P�ں���(sh��)�Č��Q�������½YՓ�����ڽo���ĺ���(sh��)![]() ��������������
��������������![]() ����
����![]() ����
����![]() �鳣��(sh��)�����t����(sh��)
�鳣��(sh��)�����t����(sh��)![]() �P���c
�P���c![]() ���Q��
���Q��
��1�����}�O�еĽYՓ�C��������(sh��)![]() �P���c
�P���c![]() ��
��
��2��������(sh��)![]() ���P���c
���P���c![]() ���Q�����P���c
���Q�����P���c![]() ���Q���Ү�
���Q���Ү�![]() �r��
�r��![]() ������
������![]() ��ֵ��
��ֵ��
����![]() �r��
�r��![]() �ı��_ʽ��
�ı��_ʽ��
�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W�`���Ͳ�����Ϣ�e��ƽ�_ | �W���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙��e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com