
【題目】已知函數![]() .
.
(1)用五點法畫出它在一個周期內的閉區間上的圖象;
(2)指出f(x)的周期、振幅、初相、對稱軸;
(3)此函數圖象由y=sinx的圖象怎樣變換得到?(注:y軸上每一豎格長為1)

【答案】(1)答案見解析;(2)答案見解析;(3)答案見解析.
【解析】試題分析:
(1)由題意結合五點法列表,據此繪制函數圖象即可;
(2)結合函數的解析式可得函數的周期為![]() ,振幅為3,初相為
,振幅為3,初相為![]() ,對稱軸方程為:
,對稱軸方程為:![]() .
.
(3)結合三角函數的變換性質可知變換過程如下:由y=sinx在[0,2π]上的圖象向左平移![]() 個單位,把橫坐標伸長為原來的2倍,把縱坐標伸長為原來的3倍,向上平移3個單位,即可得到
個單位,把橫坐標伸長為原來的2倍,把縱坐標伸長為原來的3倍,向上平移3個單位,即可得到![]() 的圖象.
的圖象.
試題解析:
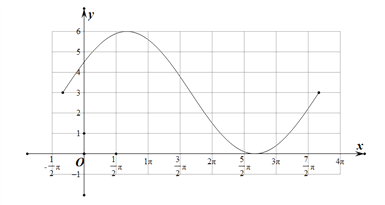
(1)令![]() 取0,
取0,![]() ,π,
,π,![]() ,2π,列表如下:
,2π,列表如下:
| 0 |
| π |
| 2π |
x |
|
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
在一個周期內的閉區間上的圖象如下圖所示:
(2)∵函數![]() 中,A=3,B=3,ω=
中,A=3,B=3,ω=![]() ,φ=
,φ=![]() .
.
∴函數f(x)的周期T=4π,振幅為3,初相為![]() ,
,
對稱軸滿足:![]() ,
,
據此可得對稱軸方程為:![]() .
.
(3)此函數圖象可由y=sinx在[0,2π]上的圖象經過如下變換得到:
①向左平移![]() 個單位,得到y=sin(x+
個單位,得到y=sin(x+![]() )的圖象;
)的圖象;
②再保持縱坐標不變,把橫坐標伸長為原來的2倍得到y=![]() 的圖象;
的圖象;
③再保持橫坐標不變,把縱坐標伸長為原來的3倍得到y=![]() 的圖象;
的圖象;
④再向上平移3個單位,得到![]() 的圖象.
的圖象.


科目:高中數學 來源: 題型:
【題目】若函數![]() 滿足:在定義域
滿足:在定義域![]() 內存在實數
內存在實數![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 為“
為“![]() 的飽和函數”.給出下列四個函數:①
的飽和函數”.給出下列四個函數:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() .其中是“
.其中是“![]() 的飽和函數”的所有函數的序號是______________.
的飽和函數”的所有函數的序號是______________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知首項為 ![]() 的等比數列{an}不是遞減數列,其前n項和為Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差數列.
的等比數列{an}不是遞減數列,其前n項和為Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差數列.
(1)求數列{an}的通項公式;
(2)若實數a使得a>Sn+ ![]() 對任意n∈N*恒成立,求a的取值范圍.
對任意n∈N*恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為  (t為參數),曲線C的極坐標方程是
(t為參數),曲線C的極坐標方程是 ![]() 以極點為原點,極軸為x軸正方向建立直角坐標系,點M(﹣1,0),直線l與曲線C交于A,B兩點.
以極點為原點,極軸為x軸正方向建立直角坐標系,點M(﹣1,0),直線l與曲線C交于A,B兩點.
(1)寫出直線l的極坐標方程與曲線C的普通方程;
(2)線段MA,MB長度分別記|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其導函數f′(x)的部分圖象如圖所示,則函數f(x)的解析式為( ) 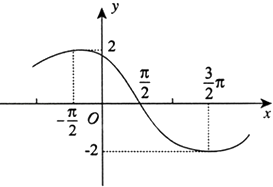
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 f(x)=x﹣ln x﹣2.
(Ⅰ)求函數 f ( x) 的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在區間(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F為雙曲線 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )
=1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )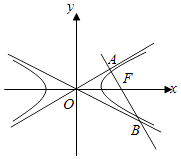
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,P是直線x=4上一動點,以P為圓心的圓Γ經定點B(1,0),直線l是圓Γ在點B處的切線,過A(﹣1,0)作圓Γ的兩條切線分別與l交于E,F兩點.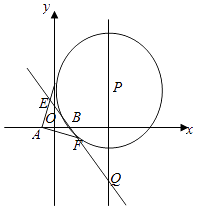
(1)求證:|EA|+|EB|為定值;
(2)設直線l交直線x=4于點Q,證明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,有2Sn=n2+n+4(n∈+)
(1)求數列的通項公式an;
(2)若bn= ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com