
【題目】已知函數![]() .
.
(1)當a=1時,求函數![]() 在(2,
在(2,![]() )處的切線方程:
)處的切線方程:
(2)當a=2時,求函數![]() 的單調區間和極值;
的單調區間和極值;
(3)若![]() 在
在![]() 上是單調增函數,求實數a的取值范圍.
上是單調增函數,求實數a的取值范圍.
【答案】(2)![]() ; (2)
; (2)![]() 在
在![]() 上單調遞增,f(x)無極值. (3)
上單調遞增,f(x)無極值. (3)![]()
【解析】
(1)當![]() 時,求導函數,則函數在
時,求導函數,則函數在![]() 處的切線的斜率即為導數值
處的切線的斜率即為導數值![]() ,根據點斜式方程即可求出切線方程;
,根據點斜式方程即可求出切線方程;
(2)先求出函數的定義域,把![]() 代入到函數中并求出
代入到函數中并求出![]() 時
時![]() 的值,在定義域內討論導函數的正負得到函數的單調區間及極值;
的值,在定義域內討論導函數的正負得到函數的單調區間及極值;
(3)把![]() 代入到
代入到![]() 中得到
中得到![]() 的解析式,求出其導函數大于0即函數單調,可設
的解析式,求出其導函數大于0即函數單調,可設![]() ,求出其導函數在
,求出其導函數在![]() 上單調遞減,求出
上單調遞減,求出![]() 的最大值,列出不等數求出解集即為
的最大值,列出不等數求出解集即為![]() 的取值范圍.
的取值范圍.
解:(1)當![]() 時,函數
時,函數![]() ,
,
則![]() ,
,
![]() 函數
函數![]() 在
在![]() 處的切線斜率為
處的切線斜率為![]()
![]() ,切點為
,切點為![]() ;
;
![]() 函數
函數![]() 在
在![]() 處的切線方程為:
處的切線方程為:![]() ;
;
即![]() ;
;
(2)函數![]() 的定義域為
的定義域為![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
則![]() ;
;
![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 無極值.
無極值.
(3)由![]() ,得
,得![]() ;
;
又函數![]() 在
在![]() 上單調增函數,
上單調增函數,
則![]() 在
在![]() 上恒成立,
上恒成立,
即不等式![]() 在
在![]() 上恒成立;
上恒成立;
也即![]() 在
在![]() 上恒成立,
上恒成立,
又![]() 在
在![]() 為減函數,
為減函數,
所以![]() (1)
(1)![]() .
.
所以![]() .
.
故![]() 的取值范圍為
的取值范圍為![]() .
.


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】對于以下四個命題:①兩條異面直線有無數條公垂線;②直線在平面內的射影是直線;③如果兩條直線在同一個平面內的射影平行,那這兩條直線平行;④過兩條異面直線的一條有且僅有一個平面與已知直線平行;上述命題中為真命題的個數為( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() 為直角,
為直角,![]() ,
,![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() .
.
(1)試用![]() 、
、![]() 表示向量
表示向量![]() ;
;
(2)在線段![]() 上取一點
上取一點![]() ,在線段
,在線段![]() 上取一點
上取一點![]() ,使得直線
,使得直線![]() 過
過![]() ,設
,設![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,過
,過![]() 作線段
作線段![]() ,使得
,使得![]() 為
為![]() 的中點,且
的中點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
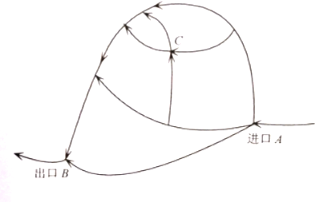
【題目】如圖是一旅游景區供游客行走的路線圖,假設從進口![]() 開始到出口
開始到出口![]() ,每遇到一個岔路口,每位游客選擇其中一條道路行進是等可能的.現有甲、乙、丙、丁共
,每遇到一個岔路口,每位游客選擇其中一條道路行進是等可能的.現有甲、乙、丙、丁共![]() 名游客結伴到旅游景區游玩,他們從進口
名游客結伴到旅游景區游玩,他們從進口![]() 的岔路口就開始選擇道路自行游玩,并按箭頭所指路線行走,最后到出口
的岔路口就開始選擇道路自行游玩,并按箭頭所指路線行走,最后到出口![]() 集中,設點
集中,設點![]() 是其中的一個交叉路口點.
是其中的一個交叉路口點.
(1)求甲經過點![]() 的概率;
的概率;
(2)設這![]() 名游客中恰有
名游客中恰有![]() 名游客都是經過點
名游客都是經過點![]() ,求隨機變量
,求隨機變量![]() 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一次足球邀請賽共安排了![]() 支球隊參加,每支球隊預定的比賽場數分別是
支球隊參加,每支球隊預定的比賽場數分別是![]() ,
,![]() ,…,
,…,![]() .若任兩支球隊之間至多安排了一場比賽,則稱
.若任兩支球隊之間至多安排了一場比賽,則稱![]() 是一個“有效安排”.證明:若
是一個“有效安排”.證明:若![]() 是一個有效安排,且
是一個有效安排,且![]() ,則可去掉一支球隊,并重新調整各隊之間的對局情況,使
,則可去掉一支球隊,并重新調整各隊之間的對局情況,使![]() 也是一個有效安排.
也是一個有效安排.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】出租車幾何學是由十九世紀的赫爾曼·閔可夫斯基所創立的.在出租車幾何學中,點還是形如![]() 的有序實數對,直線還是滿足
的有序實數對,直線還是滿足![]() 的所有
的所有![]() 組成的圖形,角度大小的定義也和原來一樣.直角坐標系內任意兩點
組成的圖形,角度大小的定義也和原來一樣.直角坐標系內任意兩點![]() ,
,![]() ,定義它們之間的一種“距離”:
,定義它們之間的一種“距離”:![]() ;到兩點P.Q“距離”相等的點的軌跡稱為線段PQ的“垂直平分線”.已知點
;到兩點P.Q“距離”相等的點的軌跡稱為線段PQ的“垂直平分線”.已知點![]() 、
、![]() 、
、![]() ,請解決以下問題:
,請解決以下問題:
(1)求線段![]()
![]() 上一點
上一點![]() 到原點
到原點![]() 的“距離”;
的“距離”;
(2)寫出線段AB的“垂直平分線”的軌跡方程,并作出大致圖像;
(3)定義:若三角形三邊的“垂直平分線”交于一點,則該點稱為三角形的“外心”.試判斷![]() 的“外心”是否存在,如果存在,求出“外心”;如果不存在,說明理由.
的“外心”是否存在,如果存在,求出“外心”;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 與點
與點![]() 在直線
在直線![]() 的兩側,給出以下結論:①
的兩側,給出以下結論:①![]() ;②當
;②當![]() 時,
時,![]() 有最小值,無最大值;③
有最小值,無最大值;③![]() ;④當
;④當![]() 且
且![]() 時,
時,![]() 的取值范圍是
的取值范圍是![]() ,正確的個數為( )
,正確的個數為( )
A.1個B.2個C.3個D.以上都不對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com