【題目】某校舉行了一次考試，從學生中隨機選取了
人的成績作為樣本進行統(tǒng)計.已知這些學生的成績?nèi)吭?/span>分至
分之間，現(xiàn)將成績按如下方式分成
組：第一組
，第二組
，.......，第六組
，并據(jù)此繪制了如圖所示的頻率分布直方圖.
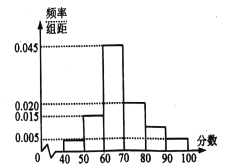
（1）估計這次月考數(shù)學成績的平均分和眾數(shù)；
（2）從成績大于等于
分的學生中隨機抽取
人，求至少有
名學生的成績在內(nèi)的概率.
【答案】（1）平均分
，眾數(shù)
；（2）
【解析】
（1）先利用頻率和為
，求得
的頻率，然后利用每組中點值作為代表，計算出平均數(shù).眾數(shù)是頻率分布直方圖最高的長方形的中點，故為.（2）分別計算出
內(nèi)的學生數(shù)，然后利用列舉法求得至少有1名學生的成績在
內(nèi)的概率.
（1）成績在
內(nèi)的頻率為：
平均分為
眾數(shù)的估計值是
（2）成績在的學生有
人，記此
人分別為
，
，
，
，
成績在
內(nèi)的學生有
人，記此
人分別為
，
，
則從這
人中任選人的基本事件有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共
個.
記事件“在成績大于等于
分的學生中隨機抽取人，至少有名學生的成績在內(nèi)”為事件
，則事件包含的基本事件有，，，，，，，，共
個.
故事件發(fā)生的概率為
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】2020年1月22日，國新辦發(fā)布消息：新型冠狀病毒來源于武漢一家海鮮市場非法銷售的野生動.專家通過全基因組比對發(fā)現(xiàn)此病毒與2003年的非典冠狀病毒以及此后的中東呼吸綜合征冠狀病毒，分別達到70%和40%的序列相似性.這種新型冠狀病毒對人們的健康生命帶來了嚴重威脅因此，某生物疫苗研究所加緊對新型冠狀病毒疫苗進行實驗，并將某一型號疫苗用在動物小白鼠身上進行科研和臨床實驗，得到統(tǒng)計數(shù)據(jù)如下：
未感染病毒 | 感染病毒 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現(xiàn)從所有試驗小白鼠中任取一只，取到“注射疫苗”小白鼠的概率為
.
（1）求
列聯(lián)表中的數(shù)據(jù)
，
，
，
的值；
（2）能否有99.9%把握認為注射此種疫苗對預防新型冠狀病毒有效？
附：
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某工廠生產(chǎn)某種產(chǎn)品的年固定成本為250萬元，每生產(chǎn)x千件，需另投入成本為C(x)，當年產(chǎn)量不足80千件時，C(x)＝
x2＋10x(萬元)．當年產(chǎn)量不小于80千件時，C(x)＝51x＋
－1 450(萬元)．每件商品售價為0.05萬元．通過市場分析，該廠生產(chǎn)的商品能全部售完．
（1）寫出年利潤L(x)(萬元)關于年產(chǎn)量x(千件)的函數(shù)解析式；
（2）當年產(chǎn)量為多少千件時，該廠在這一商品的生產(chǎn)中所獲利潤最大？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知數(shù)列
中，
，
,
.
（1）求證：數(shù)列
是等比數(shù)列；
（2）求數(shù)列的通項公式；
（3）設
，
，若對任意
，有
恒成立，求實數(shù)m的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】《情境》劉曉紅同學在做達標訓練的課外作業(yè)時，遇到一個如何用五點法作出正弦型函數(shù)在長度為一個周期的閉區(qū)間上的圖象及圖象之間如何進行變換的問題，她犯愁了．
《問題》設函數(shù)
的周期為
，且圖象過點
．
（1）求
與
的值；
（2）用五點法作函數(shù)
在長度為一個周期的閉區(qū)間上的圖象；
（3）敘述函數(shù)的圖象可由函數(shù)
的圖象經(jīng)過怎樣的變換而得到．
由于劉曉紅對上述問題還沒有掌握解決方法及解題概念和步驟，導致無從下手，于是她請教了班上的學習委員張倩同學給她做了如下點撥：
用五點法作出在一個周期的閉區(qū)間上的圖象，首先要列表并分別令相位
、
、、
、
，再解出對應的
、
的值，得出坐標
，然后描點，最后畫出圖象．而由函數(shù)的圖象變到函數(shù)
的圖象主要有兩種途徑：①按物理量初相，周期
，振幅
的順序變換；②按物理量周期，初相，振幅的順序變換．要注意兩者操作的區(qū)別，防止出錯．
經(jīng)過張倩耐心而細致的解釋，劉曉紅豁然開朗，并對該題解答如下：
（注意：解答第（3）問時，要按照題中要求，寫出兩種變換過程）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】2018年開始，直播答題突然就火了，在某場活動中，最終僅有23人平分100萬獎金，這23人可以說是“學霸”級的大神.但隨著直播答題的發(fā)展，其模式的可持續(xù)性受到了質(zhì)疑，某網(wǎng)戰(zhàn)隨機選取500名網(wǎng)民進行了調(diào)查，得到的數(shù)據(jù)如下表：
男 | 女 | |
認為直播答題模式可持續(xù) | 180 | 140 |
認為直播答題模式不可持續(xù) | 120 | 60 |
（1）根據(jù)表格中的數(shù)據(jù)，用獨立性檢驗的思維方法判斷是否有97.5%的把握認為對直播答題模式的態(tài)度與性別有關系？
（2）已知在參與調(diào)查的500人中，有15%曾參加答題游戲瓜分過獎金，而男性被調(diào)查者有12%曾參加游戲瓜分過獎金，求女性被調(diào)查者參與游戲瓜分過獎金的概率.
參考公式：
臨界值表：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，直線
與圓
相切，圓心的坐標為
．
（1）求圓的方程；
（2）設直線
與圓沒有公共點，求
的取值范圍；
（3）設直線
與圓交于
、
兩點，且
，求
的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】解答下列問題：
（1）求平行于直線3x+4y- 2=0,且與它的距離是1的直線方程；
（2）求垂直于直線x+3y -5=0且與點P( -1,0)的距離是
的直線方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
