
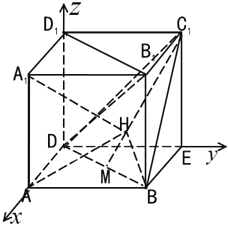
【題目】如圖,在多面體ABD﹣A1B1C1D1中四邊形A1B1C1D1,ADD1A1.ABB1A1均為正方形.點(diǎn)M是BD的中點(diǎn).點(diǎn)H在線段C1M上,且A1H與平面ABD所成角的正弦值為![]() .
.
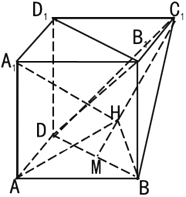
(Ⅰ)證明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
【答案】(Ⅰ)證明見(jiàn)解析 (Ⅱ)![]() .
.
【解析】
(Ⅰ)構(gòu)造正方體證明BD∥B1D1即可.
(Ⅱ)建立空間直角坐標(biāo)系,利用A1H與平面ABD所成角的正弦值為![]() 可求得
可求得![]() 的坐標(biāo),再利用空間向量求二面角的方法求解即可.
的坐標(biāo),再利用空間向量求二面角的方法求解即可.
(Ⅰ)證明:如圖,構(gòu)造正方體ABED﹣A1B1C1D1,
結(jié)合正方體ABED﹣A1B1C1D1,得BD∥B1D1,
∵BD平面BC1D,B1D1平面BC1D,
∴B1D1∥平面BC1D.
(Ⅱ)解:以D為原點(diǎn),DA為x軸,DE為y軸,DD1為z軸,建立空間直角坐標(biāo)系,
設(shè)AD=2,則M(1,1,0),C1(0,2,2),A1(2,0,2),A(2,0,0),B(2,2,0),
設(shè)H(a,b,c),![]() ,(0≤λ≤1),則(a,b﹣2,c﹣2)=(λ,﹣λ,﹣2λ),
,(0≤λ≤1),則(a,b﹣2,c﹣2)=(λ,﹣λ,﹣2λ),
∴H(λ,2﹣λ,2﹣2λ),
平面ABD的法向量![]() (0,0,1),
(0,0,1),![]() (λ﹣2,2﹣λ,﹣2λ),
(λ﹣2,2﹣λ,﹣2λ),
∵A1H與平面ABD所成角的正弦值為![]() .
.
∴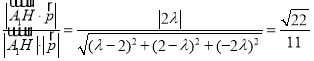 ,
,
解得![]() ,(舍負(fù)),∴H(
,(舍負(fù)),∴H(![]() ,
,![]() ,1),
,1),
![]() (
(![]() ,
,![]() ,﹣1),
,﹣1),![]() (0,0,﹣2),
(0,0,﹣2),![]() (0,2,﹣2),
(0,2,﹣2),
設(shè)平面AA1H的法向量![]() (x,y,z),
(x,y,z),
則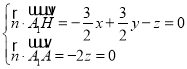 ,取x=1,得
,取x=1,得![]() (1,1,0),
(1,1,0),
設(shè)平面A1HB的法向量![]() (x,y,z),
(x,y,z),
則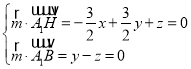 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,1),
,1,1),
設(shè)二面角A﹣A1H﹣B的平面角為θ,
則cosθ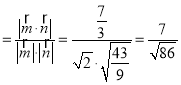 ,
,
∴二面角A﹣A1H﹣B的正弦值為:
sinθ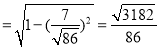 .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線上一動(dòng)點(diǎn)P(x,y)(x>0)到定點(diǎn)F(![]() ,0)的距離與它到直線l:x
,0)的距離與它到直線l:x![]() 的距離的比是
的距離的比是![]() .
.
(1)求動(dòng)點(diǎn)P的軌跡E的方程;
(2)若M是曲線E上的一個(gè)動(dòng)點(diǎn),直線l′:y=x+4,求點(diǎn)M到直線l′的距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)二階方矩陣![]() ,則矩陣
,則矩陣![]() 所對(duì)應(yīng)的矩陣變換為:
所對(duì)應(yīng)的矩陣變換為:![]() ,其意義是把點(diǎn)
,其意義是把點(diǎn)![]() 變換為點(diǎn)
變換為點(diǎn)![]() ,矩陣
,矩陣![]() 叫做變換矩陣.
叫做變換矩陣.
(1)當(dāng)變換矩陣![]() 時(shí),點(diǎn)
時(shí),點(diǎn)![]() 、
、![]() 經(jīng)矩陣變換后得到點(diǎn)分別是
經(jīng)矩陣變換后得到點(diǎn)分別是![]() 、
、![]() ,求經(jīng)過(guò)點(diǎn)
,求經(jīng)過(guò)點(diǎn)![]() 、
、![]() 的直線的點(diǎn)方向式方程;
的直線的點(diǎn)方向式方程;
(2)當(dāng)變換矩陣![]() 時(shí),若直線上的任意點(diǎn)
時(shí),若直線上的任意點(diǎn)![]() 經(jīng)矩陣變換后得到的點(diǎn)
經(jīng)矩陣變換后得到的點(diǎn)![]() 仍在該直線上,求直線的方程;
仍在該直線上,求直線的方程;
(3)若點(diǎn)![]() 經(jīng)過(guò)矩陣
經(jīng)過(guò)矩陣![]() 變換后得到點(diǎn)
變換后得到點(diǎn)![]() ,且
,且![]() 與
與![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱,求變換矩陣
對(duì)稱,求變換矩陣![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某省的一個(gè)氣象站觀測(cè)點(diǎn)在連續(xù)4天里記錄的AQI指數(shù)M與當(dāng)天的空氣水平可見(jiàn)度![]() (單位:cm)的情況如表1:
(單位:cm)的情況如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
該省某市2017年11月份AQI指數(shù)頻數(shù)分布如表2:
|
|
|
|
|
|
頻數(shù)(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)設(shè)
(2)小李在該市開(kāi)了一家洗車店,洗車店每天的平均收入與AQI指數(shù)存在相關(guān)關(guān)系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根據(jù)表3估計(jì)小李的洗車店2017年11月份每天的平均收入.
附參考公式:![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB為圓O的直徑,點(diǎn)E、F在圓O上,AB∥EF,矩形ABCD所在的平面與圓O所在的平面互相垂直.已知AB=2,EF=1.
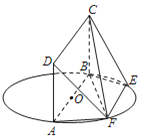
(Ⅰ)求證:平面DAF⊥平面CBF;
(Ⅱ)當(dāng)AD=1時(shí),求直線FB與平面DFC所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在等腰直角三角形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是邊
是邊![]() 上異于
上異于![]() 的一點(diǎn),光線從點(diǎn)
的一點(diǎn),光線從點(diǎn)![]() 出發(fā),經(jīng)
出發(fā),經(jīng)![]() 反射后又回到原點(diǎn)
反射后又回到原點(diǎn)![]() ,光線
,光線![]() 經(jīng)過(guò)
經(jīng)過(guò)![]() 的重心.
的重心.
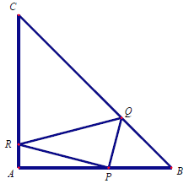
(1)建立適當(dāng)?shù)淖鴺?biāo)系,請(qǐng)求![]() 的重心
的重心![]() 的坐標(biāo);
的坐標(biāo);
(2)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)求![]() 的周長(zhǎng)及面積.
的周長(zhǎng)及面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)某校夏令營(yíng)有3名男同學(xué)A、B、C和3名女同學(xué)X、Y、Z,其年級(jí)情況如下表:
一年級(jí) | 二年級(jí) | 三年級(jí) | |
男同學(xué) | A | B | C |
女同學(xué) | X | Y | Z |
現(xiàn)從這6名同學(xué)中隨機(jī)選出2人參加知識(shí)競(jìng)賽(每人被選到的可能性相同).
①用表中字母列舉出所有可能的結(jié)果;
②設(shè)M為事件“選出的2人來(lái)自不同年級(jí)且恰有1名男同學(xué)和1名女同學(xué)”,求事件M發(fā)生的概率.
(2)節(jié)日前夕,小李在家門前的樹(shù)上掛了兩串彩燈.這兩串彩燈的第一次閃亮相互獨(dú)立,且都在通電后的4秒內(nèi)任一時(shí)刻等可能發(fā)生,然后每串彩燈以4秒為間隔閃亮.那么這兩串彩燈同時(shí)通電后,它們第一次閃亮的時(shí)刻相差不超過(guò)2秒的概率是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-4坐標(biāo)系與參數(shù)方程選講
在直角坐標(biāo)系中,以原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,已知曲線
軸的正半軸為極軸建立極坐標(biāo)系,已知曲線![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為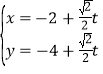 (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() ,
,![]() 兩點(diǎn).
兩點(diǎn).
(1)寫出曲線![]() 的平面直角坐標(biāo)方程和直線
的平面直角坐標(biāo)方程和直線![]() 的普通方程:
的普通方程:
(2)若![]() 成等比數(shù)列,求實(shí)數(shù)
成等比數(shù)列,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題(1)![]() 條斜線段長(zhǎng)相等,則他們?cè)谄矫鎯?nèi)的射影長(zhǎng)也相等;(2)直線
條斜線段長(zhǎng)相等,則他們?cè)谄矫鎯?nèi)的射影長(zhǎng)也相等;(2)直線![]() 不在平面
不在平面![]() 內(nèi),他們?cè)谄矫?/span>
內(nèi),他們?cè)谄矫?/span>![]() 內(nèi)的射影是兩條平行直線,則
內(nèi)的射影是兩條平行直線,則![]() ;(3)與同一平面所成的角相等的兩條直線平行;(4)一條直線與一個(gè)平面所成的角是
;(3)與同一平面所成的角相等的兩條直線平行;(4)一條直線與一個(gè)平面所成的角是![]() ,那么它與平面內(nèi)任何其他直線所成的角都不小于
,那么它與平面內(nèi)任何其他直線所成的角都不小于![]() ;其中正確的命題序號(hào)是____________.
;其中正確的命題序號(hào)是____________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com