
設(shè) 是定義在
是定義在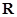 上的偶函數(shù),對任意的
上的偶函數(shù),對任意的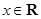 ,都有
,都有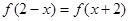 ,且當(dāng)
,且當(dāng) 時,
時, ,若關(guān)于
,若關(guān)于 的方程
的方程
 在區(qū)間
在區(qū)間 內(nèi)恰有三個不同實根,則實數(shù)
內(nèi)恰有三個不同實根,則實數(shù) 的取值范圍是 .
的取值范圍是 .
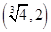
【解析】解:設(shè)x∈[0,2],則-x∈[-2,0],∴f(-x)=(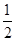 )-x-1=2x-1,
)-x-1=2x-1,
∵f(x)是定義在R上的偶函數(shù),∴f(x)=f(-x)=2x-1.
∵對任意x∈R,都有f(x)=f(x+4),
∴當(dāng)x∈[2,4]時,(x-4)∈[-2,0],∴f(x)=f(x-4)=(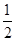 )x-4-1;
)x-4-1;
及當(dāng)x∈[4,6]時,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在區(qū)間(-2,6]內(nèi)關(guān)于x的方程f(x)-loga(x+2)=0(a>1)恰有三個不同的實數(shù)根,
∴函數(shù)y=f(x)與函數(shù)y=loga(x+2)在區(qū)間(-2,6]上恰有三個交點,通過畫圖可知:恰有三個交點的條件是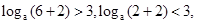 得到參數(shù)a的范圍是
得到參數(shù)a的范圍是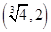 ,故答案為
,故答案為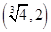


科目:高中數(shù)學(xué) 來源: 題型:
(08年長沙一中一模文)設(shè)![]() 是定義在
是定義在![]() ]上的偶函數(shù),
]上的偶函數(shù),![]() 的圖象與
的圖象與![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱,且當(dāng)
對稱,且當(dāng)![]() 時,
時,![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上為增函數(shù),求
上為增函數(shù),求![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數(shù)![]() ,使
,使![]() 的圖象的最高點落在直線
的圖象的最高點落在直線![]() 上?若存在,求出
上?若存在,求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年河南省南陽市高三9月月考理科數(shù)學(xué)試卷(解析版) 題型:填空題
設(shè) 是定義在
是定義在 上的偶函數(shù),對任意的
上的偶函數(shù),對任意的 ,都有
,都有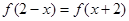 ,且當(dāng)
,且當(dāng) 時,
時, ,若關(guān)于
,若關(guān)于 的方程
的方程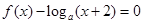
 在區(qū)間
在區(qū)間 內(nèi)恰有三個不同實根,則實數(shù)
內(nèi)恰有三個不同實根,則實數(shù) 的取值范圍是
.
的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年河北省石家莊市高三暑期第二次考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:選擇題
設(shè) 是定義在
是定義在 上的偶函數(shù),且
上的偶函數(shù),且 ,當(dāng)
,當(dāng) 時,
時, ,若在區(qū)間
,若在區(qū)間 內(nèi)關(guān)于
內(nèi)關(guān)于 的方程
的方程 ,恰有
,恰有 個不同的實數(shù)根,則實數(shù)
個不同的實數(shù)根,則實數(shù)
 的取值范圍是
的取值范圍是
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年河北省高三第一次高考仿真測試文科數(shù)學(xué)試卷(解析版) 題型:填空題
設(shè) 是定義在
是定義在 上的偶函數(shù),對任意
上的偶函數(shù),對任意 ,都有
,都有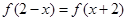 成立,且當(dāng)
成立,且當(dāng) 時,
時, .若關(guān)于
.若關(guān)于 的方程
的方程
 在區(qū)間
在區(qū)間 內(nèi)恰有兩個不同實根,則實數(shù)
內(nèi)恰有兩個不同實根,則實數(shù) 的取值范圍是
.
的取值范圍是
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com