
【題目】已知直線l的參數(shù)方程為 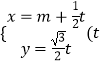 為參數(shù)),以坐標(biāo)原點為極點,以x軸正半軸為極軸建立極坐標(biāo)系,橢圓C的極坐標(biāo)方程為
為參數(shù)),以坐標(biāo)原點為極點,以x軸正半軸為極軸建立極坐標(biāo)系,橢圓C的極坐標(biāo)方程為 ![]() ,且直線l經(jīng)過橢圓C的右焦點F.
,且直線l經(jīng)過橢圓C的右焦點F.
(1)求橢圓C的內(nèi)接矩形PMNQ面積的最大值;
(2)若直線l與橢圓C交于A,B兩點,求|FA||FB|的值.
【答案】
(1)解:橢圓C化為5ρ2cos2θ+9ρ2sin2θ=45,∴5x2+9y2=45,
∴橢圓的標(biāo)準(zhǔn)方程: ![]() .設(shè)橢圓C的內(nèi)接矩形PMNQ中,P的坐標(biāo)為
.設(shè)橢圓C的內(nèi)接矩形PMNQ中,P的坐標(biāo)為 ![]() ,
,
∴ ![]() .
.
∴橢圓C的內(nèi)接矩形PMNQ面積最大值為 ![]()
(2)解:由橢圓C的方程 ![]() ,得橢圓C的右焦點F(2,0),由直線l經(jīng)過右焦點F(2,0),得m=2,
,得橢圓C的右焦點F(2,0),由直線l經(jīng)過右焦點F(2,0),得m=2,
易得直線l的參數(shù)方程可化為 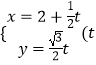 為參數(shù)),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
為參數(shù)),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
∴ ![]() ,即
,即 ![]() .
.
|FA||FB|的值 ![]()
【解析】(1)將橢圓的極坐標(biāo)方程轉(zhuǎn)化成標(biāo)準(zhǔn)方程,設(shè)P點坐標(biāo),根據(jù)二倍角公式及正弦函數(shù)的性質(zhì),即可求得橢圓C的內(nèi)接矩形PMNQ面積的最大值;(2)將參數(shù)方程代入橢圓的標(biāo)準(zhǔn)方程,由韋達(dá)定理即可求得 ![]() ,即可求得|FA||FB|的值.
,即可求得|FA||FB|的值.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在數(shù)列{an}中,a1=4,nan+1﹣(n+1)an=2n2+2n.
(Ⅰ)求證:數(shù)列 ![]() 是等差數(shù)列;
是等差數(shù)列;
(Ⅱ)求數(shù)列 ![]() 的前n項和Sn .
的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}的前n項和為Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若數(shù)列{bn}滿足 ![]() =logabn(n∈N*),求數(shù)列{(an+6)bn}的前n項和.
=logabn(n∈N*),求數(shù)列{(an+6)bn}的前n項和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某店銷售進(jìn)價為2元/件的產(chǎn)品![]() ,該店產(chǎn)品
,該店產(chǎn)品![]() 每日的銷售量
每日的銷售量![]() (單位:千件)與銷售價格
(單位:千件)與銷售價格![]() (單位:元/件)滿足關(guān)系式
(單位:元/件)滿足關(guān)系式![]() ,其中
,其中![]() .
.
(1)若產(chǎn)品![]() 銷售價格為4元/件,求該店每日銷售產(chǎn)品
銷售價格為4元/件,求該店每日銷售產(chǎn)品![]() 所獲得的利潤;
所獲得的利潤;
(2)試確定產(chǎn)品![]() 的銷售價格,使該店每日銷售產(chǎn)品
的銷售價格,使該店每日銷售產(chǎn)品![]() 所獲得的利潤最大.(保留1位小數(shù))
所獲得的利潤最大.(保留1位小數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱臺ABCD﹣A1B1C1D1中,底面ABCD為平行四邊形,∠BAD=120°,M為CD上的點.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 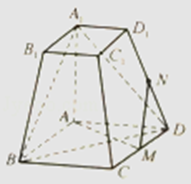
(1)求證:AM⊥A1B;
(2)若M為CD的中點,N為棱DD1上的點,且MN與平面A1BD所成角的正弦值為 ![]() ,試求DN的長.
,試求DN的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圓錐的軸截面SAB是邊長為2的等邊三角形,O為底面中心,M為SO的中點,動點P在圓錐底面內(nèi)(包括圓周).若AM⊥MP,則P點形成的軌跡的長度為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直(其中
垂直(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(Ⅰ)求![]() 的解析式及單調(diào)遞減區(qū)間;
的解析式及單調(diào)遞減區(qū)間;
(Ⅱ)若函數(shù)![]() 無零點,求
無零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國古代名著《九章算術(shù)》中有這樣一段話:“今有金錘,長五尺,斬本一尺,重四斤.?dāng)啬┮怀撸囟铮币馑际牵骸艾F(xiàn)有一根金錘,頭部的1尺,重4斤;尾部的1尺,重2斤;且從頭到尾,每一尺的重量構(gòu)成等差數(shù)列.”則下列說法錯誤的是( )
A.該金錘中間一尺重3斤
B.中間三尺的重量和是頭尾兩尺重量和的3倍
C.該金錘的重量為15斤
D.該金錘相鄰兩尺的重量之差的絕對值為0.5斤
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com