
���}Ŀ����֪�E�A![]() ��
��![]() ����һ��(g��)���c(di��n)
����һ��(g��)���c(di��n)![]() �c���タ
�c���タ![]() �Ľ��c(di��n)�غϣ��ؒ��タ�Ĝ�(zh��n)���������L(zh��ng)��1.
�Ľ��c(di��n)�غϣ��ؒ��タ�Ĝ�(zh��n)���������L(zh��ng)��1.
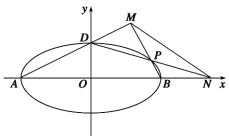
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����D��ʾ��![]() ��
��![]() ��
��![]() �ǙE�A
�ǙE�A![]() ����c(di��n)��
����c(di��n)��![]() �ǙE�A
�ǙE�A![]() �ϳ���c(di��n)�������һ�c(di��n)��ֱ��
�ϳ���c(di��n)�������һ�c(di��n)��ֱ��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ��ֱ��
��ֱ��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���O(sh��)
���O(sh��)![]() ��б�ʞ�
��б�ʞ�![]() ��
��![]() ��б�ʞ�
��б�ʞ�![]() .�C����
.�C����![]() �鶨ֵ.
�鶨ֵ.
���𰸡���1��![]() ����2��ԔҊ(ji��n)����.
����2��ԔҊ(ji��n)����.
��������
��1���əE�A�c���タ�Ľ��c(di��n)��ͬ��֪�E�A�Ľ��c(di��n)��![]() ,��
,��![]() ,�Ғ��タ�Ĝ�(zh��n)����
,�Ғ��タ�Ĝ�(zh��n)����![]() ,�������L(zh��ng)��1�ɵÙE�A�c��(zh��n)����һ��(g��)���c(di��n)��
,�������L(zh��ng)��1�ɵÙE�A�c��(zh��n)����һ��(g��)���c(di��n)��![]() ,���ɴ���E�A������,�M(j��n)����⼴�ɣ�
,���ɴ���E�A������,�M(j��n)����⼴�ɣ�
��2���ɣ�1���ɵ��c(di��n)![]() ������(bi��o),�O(sh��)ֱ��
������(bi��o),�O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ,
,![]() ��,�c�E�A����(li��n)���ɵ��c(di��n)
��,�c�E�A����(li��n)���ɵ��c(di��n)![]() ������(bi��o),��ֱ��
������(bi��o),��ֱ��![]() �ķ��̞�
�ķ��̞�![]() �cֱ��
�cֱ��![]() �ķ���(li��n)���ɵ��c(di��n)
�ķ���(li��n)���ɵ��c(di��n)![]() ������(bi��o),�ٸ���(j��)
������(bi��o),�ٸ���(j��)![]() ���c(di��n)�����ɵ��c(di��n)
���c(di��n)�����ɵ��c(di��n)![]() ������(bi��o),�������
������(bi��o),�������![]() ���
���![]() ,�M(j��n)�����C.
,�M(j��n)�����C.
��1����:���},�E�A���c(di��n)���钁�タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ,��(zh��n)�����̞�
,��(zh��n)�����̞�![]() ,
,![]() ��,
��,
�֙E�A�ؒ��タ�Ĝ�(zh��n)��![]() �������L(zh��ng)��1,
�������L(zh��ng)��1,
��ɵ�һ��(g��)���c(di��n)��![]() ,
,![]() ��,�ɢ٢ڿɵ�
��,�ɢ٢ڿɵ�![]() ,
,
�Ķ�![]() ,
,
��ԓ�E�A�ķ��̞�![]()
��2���C��:�ɣ�1���ɵ�![]() ,���c(di��n)
,���c(di��n)![]() ����E�A��c(di��n),
����E�A��c(di��n),
�t���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ,
,![]() ��,��
��,��
�۴���![]() ,���
,���![]() ,
,
��?y��n)�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
���c��(li��n)�����![]() ,
,
��![]() ,
,![]() ,
,![]() ���c(di��n)����֪
���c(di��n)����֪![]() ,��
,��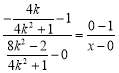 ,���
,���![]() ,
,
����![]() ��б�ʞ�
��б�ʞ�
![]() ,
,
�t![]() ����ֵ��.
����ֵ��.


 �(y��ng)���n��ͬ������(x��)ϵ�д�
�(y��ng)���n��ͬ������(x��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��һ���^(q��)��ƽ��D��һ��A�Σ�����ֱ���L(zh��ng)��![]() ���c(di��n)�ڰ�A���ϝM��
���c(di��n)�ڰ�A���ϝM��![]() ���O(sh��)
���O(sh��)![]() ���F(xi��n)Ҫ�ھ��^(q��)��(n��i)��O(sh��)һ�l�^��ͨ������
���F(xi��n)Ҫ�ھ��^(q��)��(n��i)��O(sh��)һ�l�^��ͨ������![]() ��
�� ![]() �M��.
�M��.
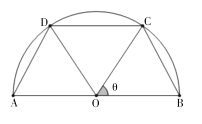
��1����![]() ��ʾ�^��ͨ�����L(zh��ng)
��ʾ�^��ͨ�����L(zh��ng)![]() �������^��ͨ��
�������^��ͨ��![]() �����ֵ��
�����ֵ��
��2���F(xi��n)Ҫ�ھ��^(q��)��(n��i)�G����������![]() �зNֲ�r������
�зNֲ�r������![]() �зNֲ����(sh��)��������
�зNֲ����(sh��)��������![]() ��(n��i)�Nֲ��ƺ����֪��λ��e��(n��i)�Nֲ�r���ͷNֲ����(sh��)������(r��n)���ǷNֲ��ƺ����(r��n)��
��(n��i)�Nֲ��ƺ����֪��λ��e��(n��i)�Nֲ�r���ͷNֲ����(sh��)������(r��n)���ǷNֲ��ƺ����(r��n)��![]() �����t��(d��ng)
�����t��(d��ng)![]() ���ֵ�r(sh��)������(r��n)���
���ֵ�r(sh��)������(r��n)���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����(du��)�ڶ��x��?y��n)�D�ĺ���(sh��)y=f��x����������څ^(q��)�g[m��n]![]() D��ͬ�r(sh��)�M�㣺
D��ͬ�r(sh��)�M�㣺
��f��x����[m��n]��(n��i)�dž��{(di��o)����(sh��)��
�ڮ�(d��ng)���x����[m��n]�r(sh��)��f��x����ֵ��Ҳ��[m��n]���t�Q(ch��ng)[m��n]��ԓ����(sh��)�ġ����C�^(q��)�g����
��1���C����[0��1]�Ǻ���(sh��)y=f��x��=x2��һ��(g��)�����C�^(q��)�g����
��2�����C������(sh��)![]() �����ڡ����C�^(q��)�g����
�����ڡ����C�^(q��)�g����
��3����֪������(sh��)![]() ��a��R��a��0���С����C�^(q��)�g��[m��n]����(d��ng)a׃���r(sh��)�����n��m�����ֵ��
��a��R��a��0���С����C�^(q��)�g��[m��n]����(d��ng)a׃���r(sh��)�����n��m�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��m��n�鳣��(sh��)������
��m��n�鳣��(sh��)������![]() ̎���о����̞�
̎���о����̞�![]() ��
��
������![]() �Ľ���ʽ����(xi��)�����x��
�Ľ���ʽ����(xi��)�����x��
������![]() ��ʹ�Ì�(du��)
��ʹ�Ì�(du��)![]() �Ϻ���
�Ϻ���![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
������![]() �Ѓɂ�(g��)��ͬ�����c(di��n)
�Ѓɂ�(g��)��ͬ�����c(di��n)![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ֱ��l�c��ֱ��y��1��x��y��7��0�քe����A��B���c(di��n)��������AB�����c(di��n)��M(1����1)���tֱ��l��б�ʞ�(����)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n)����������
�����c(di��n)����������![]() ��
��![]() ���𣬄t�����f(shu��)�����_����______________.
���𣬄t�����f(shu��)�����_����______________.
��1����Փ![]() ������λ�ã�����ƽ��
������λ�ã�����ƽ��![]() ��(n��i)��������
��(n��i)��������![]() ƽ��
ƽ��![]() ��
��
��2����Փ![]() ������λ�ã�����
������λ�ã�����![]() ��
��
��3����Փ![]() ������λ�ã�����ƽ��
������λ�ã�����ƽ��![]() ��(n��i)��������
��(n��i)��������![]() ��
��
��4���������^(gu��)���У�һ������ij��(g��)λ�ã�ʹ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���c(di��n)
���c(di��n)![]() ̎���о����̣�
̎���о����̣�
��2��������(sh��)![]() �Ѓɂ�(g��)��ͬ�Oֵ�c(di��n)����(sh��)��(sh��)
�Ѓɂ�(g��)��ͬ�Oֵ�c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3����(d��ng)![]() �r(sh��)�����C����(du��)����
�r(sh��)�����C����(du��)����![]() ��
��![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
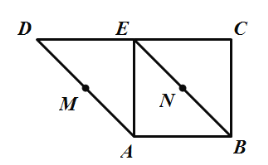
���}Ŀ����D1���ڵ�������![]() �У�
�У�![]() �քe��
�քe��![]() �����c(di��n).�F(xi��n)�քe��
�����c(di��n).�F(xi��n)�քe��![]() ��
��![]() ��
��![]() ����ʹ��ƽ��
����ʹ��ƽ��![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ���B��
���B��![]() ����D2��
����D2��
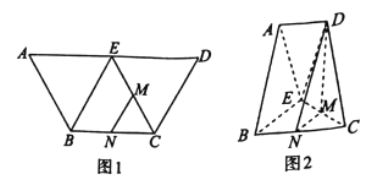
��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������w![]() ���w�e��
���w�e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)��(sh��)��![]() �Ɍ�(sh��)��(sh��)��(g��u)�ɣ��ҝM�㣺��
�Ɍ�(sh��)��(sh��)��(g��u)�ɣ��ҝM�㣺��![]() ��
��![]() ��
��![]() �����t
�����t![]() .
.
��1����![]() ��ԇ�C��
��ԇ�C��![]() ��߀������ɂ�(g��)Ԫ�أ�
��߀������ɂ�(g��)Ԫ�أ�
��2������![]() �Ƿ���pԪ�ؼ��ϣ����f(shu��)�����ɣ�
�Ƿ���pԪ�ؼ��ϣ����f(shu��)�����ɣ�
��3����![]() ��Ԫ��(g��)��(sh��)�����^(gu��)8��(g��)������Ԫ�صĺ͞�
��Ԫ��(g��)��(sh��)�����^(gu��)8��(g��)������Ԫ�صĺ͞�![]() ����
����![]() ����һ��(g��)Ԫ�ص�ƽ����������Ԫ�صķe����
����һ��(g��)Ԫ�ص�ƽ����������Ԫ�صķe����![]() .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com