
【題目】某校舉行運動會,其中三級跳遠的成績在8.0米(四舍五入,精確到0.1米)以上的進入決賽,把所得數據進行整理后,分成6組畫出頻率分布直方圖的一部分(如圖),已知從左到右前5個小組的頻率分別為0.04,0.10,0.14,0.28,0.30,第6小組的頻數是7.

(1)求進入決賽的人數;
(2)經過多次測試后發現,甲成績均勻分布在8~10米之間,乙成績均勻分布在8.5~10.5米之間,現甲,乙各跳一次,求甲比乙遠的概率.
 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知圓C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圓C2:x2+y2=1.
(1)過定點M(1,-2)作圓C2的切線,求切線的方程;
(2)若圓C1與圓C2相交,求m的取值范圍;
(3)已知點P(2,0),圓C1上一點A,圓C2上一點B,求|![]() |的最小值的取值范圍.
|的最小值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》中,將底面為直角三角形且側棱垂直于底面的三棱柱稱之為塹堵;將底面為矩形且一側棱垂直于底面的四棱錐稱之為陽馬;將四個面均為直角三角形的四面體稱之為鱉臑[biē nào].某學校科學小組為了節約材料,擬依托校園內垂直的兩面墻和地面搭建一個塹堵形的封閉的實驗室![]() ,
,![]() 是邊長為2的正方形.
是邊長為2的正方形.

(1)若![]() ,
,![]() 在
在![]() 上,四面體
上,四面體![]() 是否為鱉臑,若是,寫出其每個面的直角:若不是,請說明理由;
是否為鱉臑,若是,寫出其每個面的直角:若不是,請說明理由;
(2)當陽馬![]() 的體積最大時,求點
的體積最大時,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為方便金湖縣人民游覽三河風景區附近的“網紅橋”,現準備在河岸一側建造一個觀景臺A,已知射線PM, PN為兩邊夾角為120°的公路(長度均超過5千米),在兩條公路PM,PN上分別設立游客上下點B、C,在觀景臺A和游客上下點B、C之間和游客上下點B、C之間分別建造三條觀光線路AB,AC,BC,測得PB=3干米,PC=5千米.

(1)求線段BC的長度;
(2)若∠BAC= 60°,因政府要計算修建三條觀光線路所需費用,所以要計算AB,AC,BC三條線路的總長度的取值范圍,請你建立合適的數學模型,幫助政府解決這個問題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,底面半徑為![]() ,母線長為
,母線長為![]() 的圓柱的軸截面是四邊形
的圓柱的軸截面是四邊形![]() ,線段
,線段![]() 上的兩動點
上的兩動點![]() ,
, ![]() 滿足
滿足![]() .點
.點![]() 在底面圓
在底面圓![]() 上,且
上,且![]() ,
, ![]() 為線段
為線段![]() 的中點.
的中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱錐![]() 的體積是否為定值,若是,請求出該定值;若不是,請說明理由.
的體積是否為定值,若是,請求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2x-x2)ex-1.
(1)求函數f(x)的單調區間;
(2)若對任意x≥1,都有f(x)-mx-1+m≤0恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是兩條不同直線,
是兩條不同直線,![]() ,
,![]() 是兩個不同平面,則下列命題正確的是 ( )
是兩個不同平面,則下列命題正確的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,則
垂直于同一平面,則![]() 與
與![]() 平行
平行
B. 若![]() ,則
,則![]()
C. 若![]() ,
,![]() 不平行,則在
不平行,則在![]() 內不存在與
內不存在與![]() 平行的直線
平行的直線
D. 若![]() ,
,![]() 不平行,則
不平行,則![]() 與
與![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校研究性學習小組對該校高三學生視力情況進行調查,在高三的全體1000名學生中隨機抽取了100名學生的體檢表,得到如圖的頻率分布直方圖(圖1).

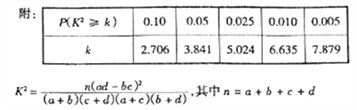
(1)若直方圖中后四組的頻數成等差數列,試估計全年級視力在5.0以下的人數;
(2)學習小組成員發現,學習成績突出的學生,近視的比較多,為了研究學生的視力與學習成績是否有關系,對年級名次在1~50名和951~1000名的學生進行了調查,得到圖2中數據,根據表中的數據,能否在犯錯誤的概率不超過0.05的前提下認為視力與學習成績有關系?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com