
【題目】隨著創(chuàng)新驅(qū)動發(fā)展戰(zhàn)略的不斷深入實(shí)施,高新技術(shù)企業(yè)在科技創(chuàng)新和經(jīng)濟(jì)發(fā)展中的帶動作用日益凸顯,某能源科學(xué)技術(shù)開發(fā)中心擬投資開發(fā)某新型能源產(chǎn)品,估計(jì)能獲得![]() 萬元的投資收益,現(xiàn)準(zhǔn)備制定一個對科研課題組的獎勵議案:獎金
萬元的投資收益,現(xiàn)準(zhǔn)備制定一個對科研課題組的獎勵議案:獎金![]() (單位:萬元)隨投資收益
(單位:萬元)隨投資收益![]() (單位:萬元)的增加而增加,獎金不超過
(單位:萬元)的增加而增加,獎金不超過![]() 萬元,同時(shí)獎金不超過投資收益的
萬元,同時(shí)獎金不超過投資收益的![]() .(即:設(shè)獎勵方案函數(shù)模擬為
.(即:設(shè)獎勵方案函數(shù)模擬為![]() 時(shí),則公司對函數(shù)模型的基本要求是:當(dāng)
時(shí),則公司對函數(shù)模型的基本要求是:當(dāng)![]() 時(shí),①
時(shí),①![]() 是增函數(shù);②
是增函數(shù);②![]() 恒成立;③
恒成立;③![]() 恒成立.)
恒成立.)
(1)現(xiàn)有兩個獎勵函數(shù)模型:(I)![]() ;(II)
;(II)![]() .試分析這兩個函數(shù)模型是否符合公司要求?
.試分析這兩個函數(shù)模型是否符合公司要求?
(2)已知函數(shù)![]() 符合公司獎勵方案函數(shù)模型要求,求實(shí)數(shù)
符合公司獎勵方案函數(shù)模型要求,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) 函數(shù)(I)不符合公司要求;(II)模型符合公司要求;(2) ![]()
【解析】
(1)分別判斷兩個函數(shù)模型是否滿足三個條件即可.
(2)由題意得函數(shù)![]() 滿足三個條件,利用函數(shù)的單調(diào)性、均值不等式可求得
滿足三個條件,利用函數(shù)的單調(diào)性、均值不等式可求得![]() 的取值范圍.
的取值范圍.
(1)對于函數(shù)模型(I):因?yàn)?/span>![]() ,即函數(shù)(I)不符合條件③,
,即函數(shù)(I)不符合條件③,
所以函數(shù)模型(I)![]() 不符合公司要求.
不符合公司要求.
對于函數(shù)模型(II):當(dāng)![]() 時(shí),
時(shí),![]() 是增函數(shù),
是增函數(shù),
且![]() ,所以
,所以![]() 恒成立.
恒成立.
設(shè)![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() .
.
所以![]() 恒成立.
恒成立.
所以函數(shù)模型(II)![]() 符合公司要求.
符合公司要求.
(2)因?yàn)?/span>![]() ,所以函數(shù)
,所以函數(shù)![]() 滿足條件①.
滿足條件①.
由函數(shù)![]() 滿足條件②得:
滿足條件②得:![]() ,所以
,所以![]() .
.
由函數(shù)![]() 滿足條件③得:
滿足條件③得:![]() 對
對![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,因?yàn)?/span>
恒成立,因?yàn)?/span>![]() ,
,
當(dāng)且僅當(dāng)![]() 時(shí)等號成立,所以
時(shí)等號成立,所以![]() .
.
綜上所述,實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若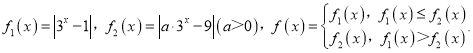
(1)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 所對應(yīng)的自變量取值區(qū)間的長度為
所對應(yīng)的自變量取值區(qū)間的長度為![]() (閉區(qū)間
(閉區(qū)間![]() 的長度為
的長度為![]() ),試求
),試求![]() 的最大值;
的最大值;
(2)是否存在這樣的![]() 使得當(dāng)
使得當(dāng)![]() 時(shí),
時(shí),![]() ?若存在,求出
?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 分別為
分別為![]() 的三內(nèi)角A,B,C的對邊,其面積
的三內(nèi)角A,B,C的對邊,其面積![]() ,在等差數(shù)列
,在等差數(shù)列![]() 中,
中,![]() ,公差
,公差![]() .?dāng)?shù)列
.?dāng)?shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若![]() ,求數(shù)列
,求數(shù)列![]() 的前n項(xiàng)和
的前n項(xiàng)和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地隨著經(jīng)濟(jì)的發(fā)展,居民收入逐年增長,如表是該地一建設(shè)銀行連續(xù)五年的儲蓄存款(年底余額),如表1
![]()
為了研究計(jì)算方便,工作人員將上表的數(shù)據(jù)進(jìn)行了處理,令![]() ,
,![]() 得到表2:
得到表2:
![]()
(1)求:![]() 關(guān)于t的線性回歸方程;
關(guān)于t的線性回歸方程;
(2)通過(1)中的方程,求出y關(guān)于![]() 的回歸方程;
的回歸方程;
(3)用所求回歸方程預(yù)測到2019年年底,該地儲蓄存款額可達(dá)多少?
附:對于線性回歸方程![]() ,其中
,其中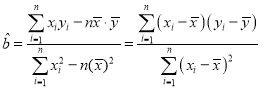 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校從參加高一年級期中考試的學(xué)生中抽出50名學(xué)生,并統(tǒng)計(jì)了她們的數(shù)學(xué)成績(成績均為整數(shù)且滿分為150分),得到的樣本頻率分布表如下:
分組 | 頻數(shù) | 頻率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 14 | 0.28 |
| 15 | 0.30 |
|
|
|
| 4 | 0.08 |
合計(jì) |
|
|
(1)在給出的樣本頻率分布表中,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估計(jì)成績在120分以上(含120分)學(xué)生的比例;
(3)抽取的50名學(xué)生中,為了幫助成績差的學(xué)生提高數(shù)學(xué)成績,學(xué)校決定成立“二幫一”小組,即從成績在![]() 的學(xué)生中選兩位同學(xué),共同幫助成績在
的學(xué)生中選兩位同學(xué),共同幫助成績在![]() 中的某一位同學(xué).已知甲同學(xué)的成績?yōu)?2分,乙同學(xué)的成績?yōu)?35分,求甲、乙兩同學(xué)恰好被安排在同一小組的概率.
中的某一位同學(xué).已知甲同學(xué)的成績?yōu)?2分,乙同學(xué)的成績?yōu)?35分,求甲、乙兩同學(xué)恰好被安排在同一小組的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 九章算術(shù)
九章算術(shù)![]() 是我國古代著名數(shù)學(xué)經(jīng)典
是我國古代著名數(shù)學(xué)經(jīng)典![]() 其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小
其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小![]() 以鋸鋸之,深一寸,鋸道長一尺
以鋸鋸之,深一寸,鋸道長一尺![]() 問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺
問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺![]() 問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示
問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示![]() 陰影部分為鑲嵌在墻體內(nèi)的部分
陰影部分為鑲嵌在墻體內(nèi)的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈
寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以原點(diǎn)
為參數(shù)),以原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() (Ⅰ)求曲線
(Ⅰ)求曲線![]() 的直角坐標(biāo)方程,并指出其表示何種曲線;(Ⅱ)設(shè)直線
的直角坐標(biāo)方程,并指出其表示何種曲線;(Ⅱ)設(shè)直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),若點(diǎn)
兩點(diǎn),若點(diǎn)![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,試求當(dāng)
,試求當(dāng)![]() 時(shí),
時(shí),![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】哥德巴赫猜想是“每個大于2的偶數(shù)可以表示為兩個素?cái)?shù)的和”,如![]() ,在不超過13的素?cái)?shù)中,隨機(jī)選取兩個不同的數(shù),其和為偶數(shù)的概率是________(用分?jǐn)?shù)表示)
,在不超過13的素?cái)?shù)中,隨機(jī)選取兩個不同的數(shù),其和為偶數(shù)的概率是________(用分?jǐn)?shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() ,雙曲線
,雙曲線![]() 的左、右焦點(diǎn)分別為F1,F2,M是雙曲線C2的一條漸近線上的點(diǎn),且OM⊥MF2,O為坐標(biāo)原點(diǎn),若
的左、右焦點(diǎn)分別為F1,F2,M是雙曲線C2的一條漸近線上的點(diǎn),且OM⊥MF2,O為坐標(biāo)原點(diǎn),若![]() ,且雙曲線C1,C2的離心率相同,則雙曲線C2的實(shí)軸長是 ( )
,且雙曲線C1,C2的離心率相同,則雙曲線C2的實(shí)軸長是 ( )
A. 32 B. 4 C. 8 D. 16
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com