
【題目】(本小題滿分12分)設函數![]() .
.
(Ⅰ)討論函數![]() 的單調性;
的單調性;
(Ⅱ)如果對所有的![]() ≥0,都有
≥0,都有![]() ≤
≤![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅲ)已知數列![]() 中,
中, ![]() ,且
,且![]() ,若數列
,若數列![]() 的前n項和為
的前n項和為![]() ,求證:
,求證:
![]() .
.
【答案】(Ⅰ)函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增;(Ⅱ)
單調遞增;(Ⅱ)![]() ;(Ⅲ)證明見解析.
;(Ⅲ)證明見解析.
【解析】試題(Ⅰ)先對函數![]() 求導,再對
求導,再對![]() 的取值范圍進行討論,即可得
的取值范圍進行討論,即可得![]() 的單調性;(Ⅱ)設
的單調性;(Ⅱ)設![]() ,先對函數
,先對函數![]() 求導,再對
求導,再對![]() 的取值范圍進行討論函數
的取值范圍進行討論函數![]() 的單調性,進而可得
的單調性,進而可得![]() 的最小值;(Ⅲ)先由已知條件求出數列
的最小值;(Ⅲ)先由已知條件求出數列![]() 的通項公式和前
的通項公式和前![]() 項和,再把
項和,再把![]() 轉化為
轉化為![]() ,由(Ⅱ)可得
,由(Ⅱ)可得![]() ,
, ![]() ,令
,令![]() ,可得
,可得![]() ,進而可證
,進而可證![]() ,即可證
,即可證![]() .
.
試題解析:(Ⅰ) ![]() 的定義域為
的定義域為![]() ,
, 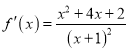 1分
1分
當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() 2分
2分
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增. 3分
單調遞增. 3分
(Ⅱ)設![]() ,則
,則
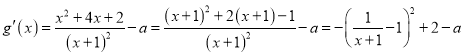
因為![]() ≥0,故
≥0,故![]() 5分
5分
(ⅰ)當![]() 時,
時, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 單調遞減,而
單調遞減,而![]() ,所以對所有的
,所以對所有的![]() ≥0,
≥0, ![]() ≤0,即
≤0,即![]() ≤
≤![]() ;
;
(ⅱ)當![]() 時,
時, ![]() ,若
,若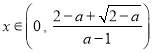 ,則
,則![]() ,
, ![]() 單調遞增,而
單調遞增,而![]() ,所以當
,所以當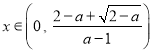 時,
時, ![]() ,即
,即![]() ;
;
(ⅲ)當![]() 時,
時, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 單調遞增,而
單調遞增,而![]() ,所以對所有的
,所以對所有的![]() ,
, ![]() ,即
,即![]() ;
;
綜上, ![]() 的最小值為2. 8分
的最小值為2. 8分
(Ⅲ)由![]() 得,
得, ![]() ,由
,由![]() 得,
得, ![]() ,
,
所以![]() ,數列
,數列![]() 是以
是以![]() 為首項,1為公差的等差數列,
為首項,1為公差的等差數列,
故![]() ,
, ![]() ,
, ![]() 9分
9分
![]()
![]()
![]()
由(Ⅱ)知![]() 時,
時, ![]() ,
, ![]() ,
,
即![]() ,
, ![]() . 10分
. 10分
法一:令![]() ,得
,得![]() ,
,
即![]()
因為![]() 11分
11分
所以![]() 12分
12分
故![]() 12分
12分
法二:
![]()
![]()
![]()
下面用數學歸納法證明.
(1)當![]() 時,令
時,令![]() 代入
代入![]() ,即得
,即得![]() ,不等式成立
,不等式成立
(2)假設![]() 時,不等式成立,即
時,不等式成立,即![]()
則![]() 時,
時, ![]()
令![]() 代入
代入![]() ,得
,得![]()
![]()
![]()
即![]()
由(1)(2)可知不等式![]() 對任何
對任何![]()
![]() 都成立.
都成立.
故![]() 12分
12分


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】如圖1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,得到如圖2所示的幾何體.
,得到如圖2所示的幾何體.
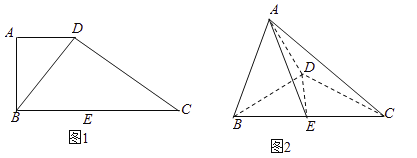
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,且
,且![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健身房為了解運動健身減肥的效果,調查了![]() 名肥胖者健身前(如直方圖(1)所示)后(如直方圖(2)所示)的體重(單位:
名肥胖者健身前(如直方圖(1)所示)后(如直方圖(2)所示)的體重(單位:![]() )變化情況:
)變化情況:
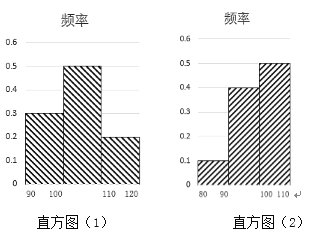
對比數據,關于這![]() 名肥胖者,下面結論正確的是( )
名肥胖者,下面結論正確的是( )
A.他們健身后,體重在區間![]() 內的人數較健身前增加了
內的人數較健身前增加了![]() 人
人
B.他們健身后,體重原在區間![]() 內的人員一定無變化
內的人員一定無變化
C.他們健身后,![]() 人的平均體重大約減少了
人的平均體重大約減少了![]()
D.他們健身后,原來體重在區間![]() 內的肥胖者體重都有減少
內的肥胖者體重都有減少
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求證:M為PB的中點;
(II)求二面角B-PD-A的大小;
(III)求直線MC與平面BDP所成角的正弦值.
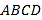
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .現以極點
.現以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系,直線
軸的非負半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為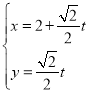 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標系方程和直線
的直角坐標系方程和直線![]() 的普通方程;
的普通方程;
(2)點![]() 在曲線
在曲線![]() 上,且到直線
上,且到直線![]() 的距離為
的距離為![]() ,求符合條件的
,求符合條件的![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com