
【題目】對于函數![]() ,若在定義域內存在實數x,滿足
,若在定義域內存在實數x,滿足![]() ,其中k為整數,則稱函數
,其中k為整數,則稱函數![]() 為定義域上的“k階局部奇函數”.
為定義域上的“k階局部奇函數”.
(1)已知函數![]() ,試判斷
,試判斷![]() 是否為
是否為![]() 上的“2階局部奇函數”?并說明理由;
上的“2階局部奇函數”?并說明理由;
(2)若![]() 是
是![]() 上的“1階局部奇函數”,求實數m的取值范圍;
上的“1階局部奇函數”,求實數m的取值范圍;
(3)若![]() ,對任意的實數
,對任意的實數![]() ,函數
,函數![]() 恒為
恒為![]() 上的“k階局部奇函數”,求整數k取值的集合.
上的“k階局部奇函數”,求整數k取值的集合.
【答案】(1)是,理由見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據題意,![]() 為
為![]() 上的“2階局部奇函數”等價于關于x的方程
上的“2階局部奇函數”等價于關于x的方程![]() 在
在![]() 上有解,列出方程,解方程即可;
上有解,列出方程,解方程即可;
(2)由“1階局部奇函數”的定義,列出方程,討論方程成立并有解時參數的取值范圍;
(3)根據“k階局部奇函數”的定義,轉化對任意的實數![]() ,函數
,函數![]() 恒為
恒為![]() 上的“k階局部奇函數”,為
上的“k階局部奇函數”,為![]() 對任意的實數
對任意的實數![]() 恒成立問題,討論二次項系數是否為零,不為零時討論
恒成立問題,討論二次項系數是否為零,不為零時討論![]() 恒成立,再令
恒成立,再令![]() ,求解
,求解![]() ,即可.
,即可.
(1)![]() 為
為![]() 上的“2階局部奇函數”等價于關于x的方程
上的“2階局部奇函數”等價于關于x的方程![]() 在
在![]() 上有解,即:
上有解,即:![]() ,
,
化簡得:![]() ,
,
解得:![]()
所以![]() 是
是![]() 上的“2階局部奇函數”.
上的“2階局部奇函數”.
(2)由![]() 是
是![]() 上的“1階局部奇函數”,
上的“1階局部奇函數”,
且![]() 要滿足
要滿足![]() ,所以
,所以![]() .
.
因為![]() 是
是![]() 上的“1階局部奇函數”,等價于關于x的方程
上的“1階局部奇函數”,等價于關于x的方程![]()
在![]() 有解,即
有解,即![]() ,化簡得:
,化簡得:![]() ,
,![]()
所以![]() ,
,
又![]() ,所以
,所以![]() .
.
(3)因為![]() 恒為R上的“k階局部奇函數”等價于關于x的方程
恒為R上的“k階局部奇函數”等價于關于x的方程![]() 恒有解.
恒有解.
即![]() ,化簡得:
,化簡得:![]() ,
,
當![]() 時,解得
時,解得![]() ,所以
,所以![]() 滿足題意;
滿足題意;
當![]() 時,
時,![]() ,即:
,即:![]() 對任意的實數
對任意的實數![]() 恒成立,
恒成立,
即![]() 對任意的實數
對任意的實數![]() 恒成立,
恒成立,
令![]() ,
,![]() 是關于t的一次函數且為
是關于t的一次函數且為![]() 上的增函數
上的增函數
則![]() ,即:
,即:![]() ,解得:
,解得:![]() 且
且![]()
綜上,整數k取值的集合![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓M: ![]() ,直線l:
,直線l:![]() ,下面五個命題,其中正確的是( )
,下面五個命題,其中正確的是( )
A.對任意實數k與θ,直線l和圓M有公共點;
B.對任意實數k與θ,直線l與圓M都相離;
C.存在實數k與θ,直線l和圓M相離;
D.對任意實數k,必存在實數θ,使得直線l與圓M相切:
E.對任意實數θ,必存在實數k,使得直線l與圓M相切;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在定義域中的實數
,若存在定義域中的實數![]() ,
,![]() 滿足
滿足![]() 且
且![]() ,則稱函數
,則稱函數![]() 為“
為“![]() 類” 函數.
類” 函數.
(1)試判斷![]() ,
,![]() 是否是“
是否是“![]() 類” 函數,并說明理由;
類” 函數,并說明理由;
(2)若函數![]() ,
,![]() ,
,![]() 為“
為“![]() 類” 函數,求
類” 函數,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來大氣污染防治工作得到各級部門的重視,某企業在現有設備下每日生產總成本![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)之間的函數關系式為
(單位:噸)之間的函數關系式為![]() ,現為了配合環境衛生綜合整治,該企業引進了除塵設備,每噸產品除塵費用為
,現為了配合環境衛生綜合整治,該企業引進了除塵設備,每噸產品除塵費用為![]() 萬元,除塵后當日產量
萬元,除塵后當日產量![]() 時,總成本
時,總成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每噸產品出廠價為48萬元,試求除塵后日產量為多少時,每噸產品的利潤最大,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校有初級教師21人,中級教師14人,高級教師7人,現采用分層抽樣的方法從這些教師中抽取6人對績效工資情況進行調查.
(1)求應從初級教師,中級教師,高級教師中分別抽取的人數;
(2)若從抽取的6名教師中隨機抽取2名做進一步數據分析,求抽取的2名均為初級教師的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,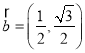 ,函數
,函數![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的方程
的方程![]() 在
在![]() 上有兩個不同的實數根
上有兩個不同的實數根![]() ,求正數
,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com