
【題目】若數列各項均非零,且存在常數![]() ,對任意
,對任意![]() ,
,![]() 恒成立,則成這樣的數列為“類等比數列”,例如等比數列一定為類等比數列,則:
恒成立,則成這樣的數列為“類等比數列”,例如等比數列一定為類等比數列,則:
(1)各項均非零的等差數列是否可能為“類等比數列”?若可能,請舉例;若不能,說明理由;
(2)已知數列![]() 為“類等比數列”,且
為“類等比數列”,且![]() ,是否存在常數
,是否存在常數![]() ,使得
,使得![]() 恒成立?
恒成立?
(3)已知數列![]() 為“類等比數列”,且
為“類等比數列”,且![]() ,求
,求![]() .
.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】根據統計,某蔬菜基地西紅柿畝產量的增加量![]() (百千克)與某種液體肥料每畝使用量
(百千克)與某種液體肥料每畝使用量![]() (千克)之間的對應數據的散點圖,如圖所示.
(千克)之間的對應數據的散點圖,如圖所示.
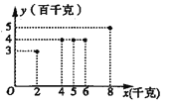
(1)依據數據的散點圖可以看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請計算相關系數
的關系,請計算相關系數![]() 并加以說明(若
并加以說明(若![]() ,則線性相關程度很高,可用線性回歸模型擬合);
,則線性相關程度很高,可用線性回歸模型擬合);
(2)求![]() 關于
關于![]() 的回歸方程,并預測液體肥料每畝使用量為12千克時,西紅柿畝產量的增加量
的回歸方程,并預測液體肥料每畝使用量為12千克時,西紅柿畝產量的增加量![]() 約為多少?
約為多少?
附:相關系數公式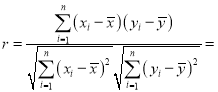
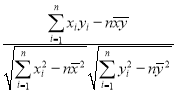 ,參考數據:
,參考數據:![]() ,
,![]() .
.
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: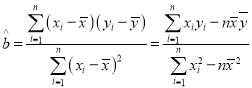 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過
經過![]() 兩點,且圓心
兩點,且圓心![]() 在直線
在直線![]() 上.
上.

(1)求圓![]() 的方程;
的方程;
(2)已知過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交截得的弦長為
相交截得的弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)已知點![]() ,在平面內是否存在異于點
,在平面內是否存在異于點![]() 的定點
的定點![]() ,對于圓
,對于圓![]() 上的任意動點
上的任意動點![]() ,都有
,都有![]() 為定值?若存在求出定點
為定值?若存在求出定點![]() 的坐標,若不存在說明理由.
的坐標,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() (
(![]() 為非零常數)與
為非零常數)與![]() 軸不垂直的直線
軸不垂直的直線![]() 與C交于
與C交于![]() 兩點.
兩點.
(1)求證:![]() (
(![]() 是坐標原點);
是坐標原點);
(2)AB的垂直平分線與![]() 軸交于
軸交于![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)設A關于![]() 軸的對稱點為D,求證:直線BD過定點,并求出定點的坐標.
軸的對稱點為D,求證:直線BD過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若存在實數![]() 使得
使得![]() 則稱
則稱![]() 是區間
是區間![]() 的
的![]() 一內點.
一內點.
(1)求證:![]() 的充要條件是存在
的充要條件是存在![]() 使得
使得![]() 是區間
是區間![]() 的
的![]() 一內點;
一內點;
(2)若實數![]() 滿足:
滿足:![]() 求證:存在
求證:存在![]() ,使得
,使得![]() 是區間
是區間![]() 的
的![]() 一內點;
一內點;
(3)給定實數![]() ,若對于任意區間
,若對于任意區間![]() ,
,![]() 是區間的
是區間的![]() 一內點,
一內點,![]() 是區間的
是區間的![]() 一內點,且不等式
一內點,且不等式![]() 和不等式
和不等式![]() 對于任意
對于任意![]() 都恒成立,求證:
都恒成立,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要條件
”成立的充分不必要條件
B. 命題![]() ,則
,則![]()
C. 為了了解800名學生對學校某項教改試驗的意見,用系統抽樣的方法從中抽取一個容量為40的樣本,則分組的組距為40
D. 已知回歸直線的斜率的估計值為1.23,樣本點的中心為![]() ,則回歸直線方程為
,則回歸直線方程為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com