
【題目】設(shè)函數(shù)![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,若
,若![]() 在
在![]() 上恒成立,求a的取值范圍.
上恒成立,求a的取值范圍.
【答案】(1)當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單遞增;當(dāng)
上單遞增;當(dāng)![]() 時(shí),
時(shí),![]() 在
在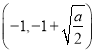 上單調(diào)遞減,
上單調(diào)遞減,![]() 在
在 上單調(diào)遞增;(2)
上單調(diào)遞增;(2)![]()
【解析】
(1)求導(dǎo),對參數(shù)進(jìn)行分類討論,根據(jù)導(dǎo)數(shù)的正負(fù)即可容易判斷函數(shù)單調(diào)性;
(2)對參數(shù)進(jìn)行分類討論,根據(jù)函數(shù)的單調(diào)性,結(jié)合函數(shù)的最值,即可求得結(jié)果.
(1)![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,
,![]()
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上恒成立,此時(shí)
上恒成立,此時(shí)![]() 在
在![]() 上單遞增;
上單遞增;
當(dāng)![]() 時(shí),令
時(shí),令![]() 得
得![]() 或
或![]() (舍去)
(舍去)
當(dāng)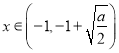 時(shí),
時(shí),![]() ,此時(shí)
,此時(shí)![]() 單調(diào)遞減
單調(diào)遞減
當(dāng)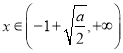 時(shí),
時(shí),![]() ,此時(shí)
,此時(shí)![]() 單調(diào)遞增
單調(diào)遞增
綜上:當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單遞增
上單遞增
當(dāng)![]() 時(shí),
時(shí),![]() 在
在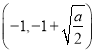 上單調(diào)遞減
上單調(diào)遞減
![]() 在
在 上單調(diào)遞增
上單調(diào)遞增
(2)由題意,![]() 在
在![]() 上恒成立.
上恒成立.
①若![]() ,
,![]()
![]()
![]()
令![]() ,
,![]() ,則
,則![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() 成立,
成立,
故![]() 時(shí),
時(shí),![]() 成立.
成立.
②若![]() 時(shí),令
時(shí),令![]() ,
,![]() ,
,
![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增![]() ﹐即有
﹐即有![]() .
.
![]() ,即
,即![]()
要使![]() 成立,必有
成立,必有![]() 成立.
成立.
由(1)可知,![]() 時(shí),
時(shí), ,又
,又![]() ,
,
則必有![]() ,得
,得![]() .
.
此時(shí),
![]()
![]()
令![]()
![]()


即![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]()
故![]() 時(shí),
時(shí),![]() 成立.
成立.
綜上,a的取值范圍是![]() .
.


 中考解讀考點(diǎn)精練系列答案
中考解讀考點(diǎn)精練系列答案 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為抗擊新冠病毒,某部門安排甲、乙、丙、丁、戊五名專家到三地指導(dǎo)防疫工作.因工作需要,每地至少需安排一名專家,其中甲、乙兩名專家必須安排在同一地工作,丙、丁兩名專家不能安排在同一地工作,則不同的分配方法總數(shù)為( )
A.18B.24C.30D.36
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,準(zhǔn)線為
,準(zhǔn)線為![]() ,
,![]() 為過焦點(diǎn)
為過焦點(diǎn)![]() 且垂直于
且垂直于![]() 軸的拋物線
軸的拋物線![]() 的弦,已知以
的弦,已知以![]() 為直徑的圓經(jīng)過點(diǎn)
為直徑的圓經(jīng)過點(diǎn)![]() .
.
(1)求![]() 的值及該圓的方程;
的值及該圓的方程;
(2)設(shè)![]() 為
為![]() 上任意一點(diǎn),過點(diǎn)
上任意一點(diǎn),過點(diǎn)![]() 作
作![]() 的切線,切點(diǎn)為
的切線,切點(diǎn)為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019冠狀病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠狀病毒(2019-nCoV)引發(fā)的疾病,目前全球感染者以百萬計(jì),我國在黨中央、國務(wù)院、中央軍委的堅(jiān)強(qiáng)領(lǐng)導(dǎo)下,已經(jīng)率先控制住疫情,但目前疫情防控形勢依然嚴(yán)峻,湖北省中小學(xué)依然延期開學(xué),所有學(xué)生按照停課不停學(xué)的要求,居家學(xué)習(xí).小李同學(xué)在居家學(xué)習(xí)期間,從網(wǎng)上購買了一套高考數(shù)學(xué)沖刺模擬試卷,快遞員計(jì)劃在下午4:00~5:00之間送貨到小區(qū)門口的快遞柜中,小李同學(xué)父親參加防疫志愿服務(wù),按規(guī)定,他換班回家的時(shí)間在下午4:30~5:00,則小李父親收到試卷無需等待的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左焦點(diǎn)為F,點(diǎn)
的左焦點(diǎn)為F,點(diǎn)![]() ,過M的直線與橢圓E交于A,B兩點(diǎn),線段AB中點(diǎn)為C,設(shè)橢圓E在A,B兩點(diǎn)處的切線相交于點(diǎn)P,O為坐標(biāo)原點(diǎn).
,過M的直線與橢圓E交于A,B兩點(diǎn),線段AB中點(diǎn)為C,設(shè)橢圓E在A,B兩點(diǎn)處的切線相交于點(diǎn)P,O為坐標(biāo)原點(diǎn).
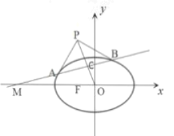
(1)證明:O、C、P三點(diǎn)共線;
(2)已知![]() 是拋物線
是拋物線![]() 的弦,所在直線過該拋物線的準(zhǔn)線與y軸的交點(diǎn),
的弦,所在直線過該拋物線的準(zhǔn)線與y軸的交點(diǎn),![]() 是弦
是弦![]() 在兩端點(diǎn)處的切線的交點(diǎn),小明同學(xué)猜想:
在兩端點(diǎn)處的切線的交點(diǎn),小明同學(xué)猜想:![]() 在定直線上.你認(rèn)為小明猜想合理嗎?若合理,請寫出
在定直線上.你認(rèn)為小明猜想合理嗎?若合理,請寫出![]() 所在直線方程;若不合理,請說明理由.
所在直線方程;若不合理,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]()
![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間與極值.
的單調(diào)區(qū)間與極值.
(2)當(dāng)![]() 時(shí),是否存在
時(shí),是否存在![]() ,使得
,使得![]() 成立?若存在,求實(shí)數(shù)
成立?若存在,求實(shí)數(shù)![]() 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A,B是橢圓C:![]() )的左右頂點(diǎn),P點(diǎn)為橢圓C上一點(diǎn),點(diǎn)P關(guān)于x軸的對稱點(diǎn)為H,且
)的左右頂點(diǎn),P點(diǎn)為橢圓C上一點(diǎn),點(diǎn)P關(guān)于x軸的對稱點(diǎn)為H,且![]()
(1)若橢圓C經(jīng)過了圓![]() 的圓心,求橢圓C的標(biāo)準(zhǔn)方程;
的圓心,求橢圓C的標(biāo)準(zhǔn)方程;
(2)在(1)的條件下,拋物線D:![]() 的焦點(diǎn)F與點(diǎn)
的焦點(diǎn)F與點(diǎn)![]() 關(guān)于y軸上某點(diǎn)對稱,且拋物線D與橢圓C在第四象限交于點(diǎn)Q,過點(diǎn)Q作直線與拋物線D有唯一公共點(diǎn),求該直線與兩坐標(biāo)軸圍成的三角形面積.
關(guān)于y軸上某點(diǎn)對稱,且拋物線D與橢圓C在第四象限交于點(diǎn)Q,過點(diǎn)Q作直線與拋物線D有唯一公共點(diǎn),求該直線與兩坐標(biāo)軸圍成的三角形面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com