
【題目】已知曲線C上任意一點M到點F(0,1)的距離比它到直線 ![]() 的距離小1.
的距離小1.
(1)求曲線C的方程;
(2)過點 P(2,2)的直線m與曲線C交于A,B兩點,設![]() 當△AOB的面積為4時(O為坐標原點),求
當△AOB的面積為4時(O為坐標原點),求 ![]() 的值.
的值.
【答案】
(1)
【解答】 點M到點F(1.0)的距離比它到直線![]() 的距離小于1,
的距離小于1,
∴點M在直線l的上方,點M到F(1,0)的距離與它到直線 ![]() 的距離相等 所以點M的軌跡C是以F為焦點,l'為準線的拋物線 ,所以曲線C的方程為x2=4y .
的距離相等 所以點M的軌跡C是以F為焦點,l'為準線的拋物線 ,所以曲線C的方程為x2=4y .
(2)
【解答】當直線m的斜率不存在時,它與曲線C只有一個交點,不合題意,
設直線m的方程為 ![]() ,代入
,代入 ![]() (*)
(*)
![]() ,對
,對![]() 恒成立,所以直線m與曲線C恒有兩個不同的交點設交點A,B的坐標分別為
恒成立,所以直線m與曲線C恒有兩個不同的交點設交點A,B的坐標分別為 ![]() ,
,
則 ![]()
所以![]()
點O到直線m的距離 ![]() ,
,
![]()
所以![]()
所以![]() 或
或![]() (舍去)
(舍去)
![]() 或
或![]()
當 ![]() 是, 方程(*)的解為
是, 方程(*)的解為 ![]() ,
,![]() 或
或![]()
當 ![]() 時 方程(☆)的解為
時 方程(☆)的解為 ![]()
![]()
【解析】(1)由題設知:點M的軌跡C是以F為焦點,l′為準線的拋物線,由此能求出曲線C的方程.(2)設直線m的方程為y=kx+(2-2k),代入x2=4y,得x2-4kx+8(k-1)=0,由△=16(k2-2k+2)>0對k∈R恒成立,知直線m與曲線C恒有兩個不同的交點,再由韋達定理、弦長公式、點到直線的距離公式,利用 ![]() 、△AOB的面積為4
、△AOB的面積為4 ,能求出λ的值.


科目:高中數學 來源: 題型:
【題目】設集合S={A0 , A1 , A2 , A3},在S上定義運算⊕:Ai⊕Aj=Ak , 其中k為i+j被4除的余數,i,j=0,1,2,3,則使關系式(Ai⊕Ai)⊕Aj=A0成立的有序數對(i,j)的組數為( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() ,函數 f(x)=x2(x-a) ,若f'(1)=1 .
,函數 f(x)=x2(x-a) ,若f'(1)=1 .
(1)求 a 的值并求曲線 y=f(x) 在點(1,f(1)) 處的切線方程y=g(x) ;
(2)設h(x)=f'(x)+g(x) ,求 h(x) 在 [0,1] 上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,兩個橢圓![]() ,
, ![]() 內部重疊區域的邊界記為曲線C,P是曲線C上的任意一點,給出下列四個判斷:
內部重疊區域的邊界記為曲線C,P是曲線C上的任意一點,給出下列四個判斷:
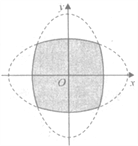
①P到F1(-4,0)、F2(4,0)、E1(0,-4)、E2(0,4)四點的距離之和為定值;
②曲線C關于直線y=x、y=-x均對稱;③曲線C所圍區域面積必小于36.
④曲線C總長度不大于6π.上述判斷中正確命題的序號為________________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點M(x,y)到直線l:x=4的距離是它到點N(1,0)的距離的2倍.
(1)求動點M的軌跡C的方程;
(2)過點P(0,3)的直線m與軌跡C交于A,B兩點.若A是PB的中點,求直線m的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,是函數y=f(x)的導函數f′(x)的圖象,則下面判斷正確的是( ) 
A.在區間(﹣2,1)上f(x)是增函數
B.在(1,3)上f(x)是減函數
C.在(4,5)上f(x)是增函數
D.當x=4時,f(x)取極大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com