
【題目】如圖,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=![]() ,點E在A1D上
,點E在A1D上
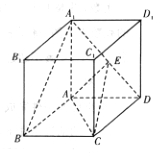
(1)求證:AA1⊥平面ABCD;
(2)當E為線段A1D的中點時,求點A1到平面EAC的距離
【答案】(1)見證明;(2)![]()
【解析】
(1)根據(jù)題中所給的數(shù)據(jù),由勾股定理得![]() 由線面垂直的判定定理即得到證明;(2)設(shè)
由線面垂直的判定定理即得到證明;(2)設(shè)![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() ,當E為A1D的中點時,可得
,當E為A1D的中點時,可得![]() 平面
平面![]() ,得點
,得點![]() 到面
到面![]() 的距離可轉(zhuǎn)為點
的距離可轉(zhuǎn)為點![]() 到平面
到平面![]() 的距離,然后利用等體積轉(zhuǎn)化即可得到答案.
的距離,然后利用等體積轉(zhuǎn)化即可得到答案.
(1)證明:![]() 底面
底面![]() 是菱形,
是菱形,![]()
在![]() 中,由
中,由![]() 知
知![]() ,
,
同理,![]() ,
,
又![]() 平面
平面![]() .
.
(2)解:設(shè)![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 為
為![]() 的中點時,連接
的中點時,連接![]() ,
,
則![]() 平面
平面![]() ,
,
直線![]() 與平面
與平面![]() 之間的距離等于點
之間的距離等于點![]() 到平面
到平面![]() 的距離,可轉(zhuǎn)化為點
的距離,可轉(zhuǎn)化為點![]() 到平面
到平面![]() 的距離,
的距離,

過點![]() 作
作![]() 于
于![]() 點
點![]() 為
為![]() 的中點,
的中點,![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點,連接
的中點,連接![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() , 又
, 又![]() ,
,
![]() ,
,
設(shè)![]() 表示點
表示點![]() 到平面
到平面![]() 的距離,則
的距離,則![]() ,
,
![]() 點
點![]() 到平面
到平面![]() 的距離為
的距離為![]()


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,那么下列結(jié)論中錯誤的是( )
,那么下列結(jié)論中錯誤的是( )
A. 若![]() 是
是![]() 的極小值點,則
的極小值點,則![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減
上單調(diào)遞減
B. ![]() ,使
,使![]()
C. 函數(shù)![]() 的圖像可以是中心對稱圖形
的圖像可以是中心對稱圖形
D. 若![]() 是
是![]() 的極值點,則
的極值點,則![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() 外的有一點
外的有一點![]() ,過點
,過點![]() 作直線
作直線![]() .
.
(1)當直線![]() 過圓心
過圓心![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(2)當直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(3)當直線![]() 的傾斜角為
的傾斜角為![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 所截得的弦長.
所截得的弦長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以該直角坐標系的原點
為參數(shù)),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設(shè)直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程:在平面直角坐標系![]() 中,曲線
中,曲線![]() :
:![]() (
(![]() 為參數(shù)),在以平面直角坐標系的原點為極點、
為參數(shù)),在以平面直角坐標系的原點為極點、![]() 軸的正半軸為極軸,且與平面直角坐標系
軸的正半軸為極軸,且與平面直角坐標系![]() 取相同單位長度的極坐標系中,曲線
取相同單位長度的極坐標系中,曲線![]() :
:![]() .
.
(1)求曲線![]() 的普通方程以及曲線
的普通方程以及曲線![]() 的平面直角坐標方程;
的平面直角坐標方程;
(2)若曲線![]() 上恰好存在三個不同的點到曲線
上恰好存在三個不同的點到曲線![]() 的距離相等,求這三個點的極坐標.
的距離相等,求這三個點的極坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖是我國古代數(shù)學家趙爽在為《周髀算經(jīng)》作注解時給出的“弦圖”.現(xiàn)提供4種顏色給“弦圖”的5個區(qū)域涂色,規(guī)定每個區(qū)域只涂一種顏色,相鄰區(qū)域顏色不相同,則不同的涂色方案共有( )
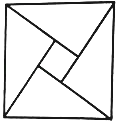
A.48種B.72種C.96種D.144種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】根據(jù)國際海洋安全規(guī)定:兩國軍艦正常狀況下(聯(lián)合軍演除外),在公海上的安全距離為20![]() (即距離不得小于20
(即距離不得小于20![]() ),否則違反了國際海洋安全規(guī)定.如圖,在某公海區(qū)域有兩條相交成60°的直航線
),否則違反了國際海洋安全規(guī)定.如圖,在某公海區(qū)域有兩條相交成60°的直航線![]() ,
,![]() ,交點是
,交點是![]() ,現(xiàn)有兩國的軍艦甲,乙分別在
,現(xiàn)有兩國的軍艦甲,乙分別在![]() ,
,![]() 上的
上的![]() ,
,![]() 處,起初
處,起初![]() ,
,![]() ,后來軍艦甲沿
,后來軍艦甲沿![]() 的方向,乙軍艦沿
的方向,乙軍艦沿![]() 的方向,同時以40
的方向,同時以40![]() 的速度航行.
的速度航行.
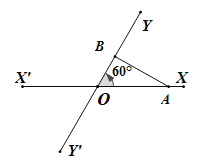
(1)起初兩軍艦的距離為多少?
(2)試判斷這兩艘軍艦是否會違反國際海洋安全規(guī)定?并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com