
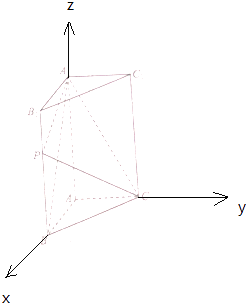
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,底面△ABC是直角三角形,AB=AC=1,點P是棱BB1上一點,滿足 ![]() (0≤λ≤1).
(0≤λ≤1). 
(1)若λ= ![]() ,求直線PC與平面A1BC所成角的正弦值;
,求直線PC與平面A1BC所成角的正弦值;
(2)若二面角P﹣A1C﹣B的正弦值為 ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:以A為坐標原點O,分別以AB,AC,AA1所在直線為x軸、y軸、z軸,
建立空間直角坐標系O﹣xyz.
∵AB=AC=1,AA1=2,則A(0,0,0),B(1,0,0),C(0,1,0),
A1(0,0,2),B1(1,0,2),P(1,0,2λ)
由 ![]() 得,
得, ![]() ,
, ![]() ,
, ![]() ,
,
設平面A1BC的法向量為 ![]() =(x1,y1,z1),由
=(x1,y1,z1),由 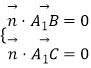 ,得
,得 ![]()
取z1=1,則x1=y1=2,從而平面A1BC的一個法向量為 ![]() =(2,2,1).
=(2,2,1).
設直線PC與平面A1BC所成的角為θ,
則sinθ=|cos< ![]() ,
, ![]() >|=
>|=  =
= ![]() ,
,
∴直線PC與平面A1BC所成的角的正弦值為 ![]()
(2)解:設平面PA1C的法向量為 ![]() =(x2,y2,z2),
=(x2,y2,z2), ![]() ,
,
由 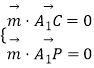 ,得
,得 ![]()
取z2=1,則x2=2﹣2λ,y2=2,平面PA1C的法向量為 ![]() =(2﹣2λ,2,1).
=(2﹣2λ,2,1).
則cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
又∵二面角P﹣A1C﹣B的正弦值為 ![]() ,∴
,∴ ![]()
化簡得λ2+8λ﹣9=0,解得λ=1或λ=﹣9(舍去),
故λ的值為1.
【解析】(1)以A為坐標原點O,分別以AB,AC,AA1所在直線為x軸、y軸、z軸,建立空間直角坐標系O﹣xyz,利用向量法能求出直線PC與平面A1BC所成的角的正弦值.(2)求出平面PA1C的法向量和平面PA1C的法向量,利用向量法能求出λ的值.
【考點精析】根據題目的已知條件,利用空間角的異面直線所成的角的相關知識可以得到問題的答案,需要掌握已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則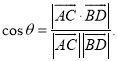 .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】(I)已知函數f(x)=rx﹣xr+(1﹣r)(x>0),其中r為有理數,且0<r<1.求f(x)的最小值;
(II)試用(I)的結果證明如下命題:設a1≥0,a2≥0,b1 , b2為正有理數,若b1+b2=1,則a1b1a2b2≤a1b1+a2b2;
(III)請將(II)中的命題推廣到一般形式,并用數學歸納法證明你所推廣的命題.注:當α為正有理數時,有求導公式(xα)r=αxα﹣1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,P是⊙O外一點,PA是切線,A為切點,割線PBC與⊙O相交于點B,C,PC=2PA,D為PC的中點,AD的延長線交⊙O于點E,證明:
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(x0,3)與點Q(x0,4)分別在橢圓![]() =1與拋物線y2=2px(p>0)上.
=1與拋物線y2=2px(p>0)上.
(1)求拋物線的方程;
(2)設點A(x1,y1),B(x2,y2)(y1≤0,y2≤0)是拋物線上的兩點,∠AQB的角平分線與x軸垂直,求直線AB在y軸上的截距的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列{an}的首項a1=1,sn是數列{an}的前n項和,且滿足:
anSn+1﹣an+1Sn+an﹣an+1=λanan+1(λ≠0,n∈N )
(1)若a1 , a2 , a3成等比數列,求實數λ的值;
(2)若λ= ![]() ,求Sn .
,求Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國式過馬路”存在很大的交通安全隱患.某調查機構為了解路人對“中國式過馬路”的態度是否與性別有關,從馬路旁隨機抽取30名路人進行了問卷調查,得到了如下列聯表:
項目 | 男性 | 女性 | 總計 |
反感 | 10 | ||
不反感 | 8 | ||
總計 | 30 |
已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)請將上面的列聯表補充完整(直接寫結果,不需要寫求解過程),并據此資料分析反感“中國式過馬路”與性別是否有關?
(2)若從這30人中的女性路人中隨機抽取2人參加一活動,記反感“中國式過馬路”的人數為X,求X的分布列和數學期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}各項均為正數,其前n項和為Sn,且滿足4Sn=(an+1)2.
(1)求{an}的通項公式;
(2)設![]() ,數列{bn}的前n項和為Tn,求Tn.
,數列{bn}的前n項和為Tn,求Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的離心率是
的離心率是![]() ,一個頂點是
,一個頂點是![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() ,
,![]() 是橢圓
是橢圓![]() 上異于點
上異于點![]() 的任意兩點,且
的任意兩點,且![]() .試問:直線
.試問:直線![]() 是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相對統一的和諧美,定義:能夠將圓![]() 的周長和面積同時等分成兩個部分的函數稱為圓
的周長和面積同時等分成兩個部分的函數稱為圓![]() 的一個“太極函數”,則下列有關說法中:
的一個“太極函數”,則下列有關說法中:

①對于圓![]() 的所有非常數函數的太極函數中,一定不能為偶函數;
的所有非常數函數的太極函數中,一定不能為偶函數;
②函數![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() 的太極函數;
的太極函數;
⑤若函數![]() 是圓
是圓![]() 的太極函數,則
的太極函數,則![]()
所有正確的是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com