
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ��
��![]() ��
��![]() �քe��E�A
�քe��E�A![]() ��������c(di��n)����
��������c(di��n)����![]() .
.

��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�c(di��n)![]() �ڙE�A
�ڙE�A![]() ��(n��i)���M(m��n)��ֱ��(xi��n)
��(n��i)���M(m��n)��ֱ��(xi��n)![]() ��
��![]() ��б�ʳ˷e��
��б�ʳ˷e��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() ��
��![]() �քe���E�A
�քe���E�A![]() ���c(di��n)
���c(di��n)![]() ��
��![]() .
.
����![]() ��
��![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q(ch��ng)����ֱ��(xi��n)
�S��(du��)�Q(ch��ng)����ֱ��(xi��n)![]() ��б�ʣ�
��б�ʣ�
����![]() ��
��![]() ����e�քe��
����e�քe��![]() ����
����![]() .
.
���𰸡���1��![]() .��2����
.��2����![]() ����
����![]() .
.
��������
��1����![]() ֪��
֪��![]() ���֙E�A
���֙E�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() �����Ԍ��c(di��n)����E�A������⼴��. ��2�����O(sh��)ֱ��(xi��n)
�����Ԍ��c(di��n)����E�A������⼴��. ��2�����O(sh��)ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ���tֱ��(xi��n)
���tֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ���c�E�A(li��n)�������M�c(di��n)����(bi��o)����ֱ��(xi��n)
���c�E�A(li��n)�������M�c(di��n)����(bi��o)����ֱ��(xi��n)![]() ��
��![]() ��б�ʳ˷e��
��б�ʳ˷e��![]() ����ֱ֪��(xi��n)
����ֱ֪��(xi��n)![]() �ķ���
�ķ���![]() ���Ķ������N�c(di��n)����(bi��o)������
���Ķ������N�c(di��n)����(bi��o)������![]() ��
��![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q(ch��ng)���г���ʽ
�S��(du��)�Q(ch��ng)���г���ʽ![]() ���Ķ����
���Ķ����![]() ��ֵ. ��2����������������e��ʽ����
��ֵ. ��2����������������e��ʽ����![]() �D(zhu��n)����
�D(zhu��n)����![]() �������c(di��n)����(bi��o)Ӌ(j��)�������Y(ji��)��.
�������c(di��n)����(bi��o)Ӌ(j��)�������Y(ji��)��.
��1����![]() ֪��
֪��![]() ��
��
�֙E�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ������
������![]() ��
��
���![]() ���ԙE�A
���ԙE�A![]() �ķ��̞�
�ķ��̞�![]() .
.
��2���O(sh��)ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ���tֱ��(xi��n)
���tֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() .
.
(li��n)��![]()
��ȥ![]() �������ã�
�������ã�![]() ��
��
���![]() ��
��![]() ������
������![]() .
.
��?y��n)�ֱ��(xi��n)![]() ��
��![]() ��б�ʳ˷e��
��б�ʳ˷e��![]() ������ֱ��(xi��n)
������ֱ��(xi��n)![]() �ķ���
�ķ���![]() .
.
(li��n)��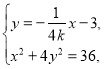 ��ȥ
��ȥ![]() �������ã�
�������ã�![]() ��
��
���![]() ��
��![]() ������
������![]() .
.
����?y��n)?/span>![]() ��
��![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q(ch��ng)������
�S��(du��)�Q(ch��ng)������![]() ��
��
��![]() �����
�����
![]() .
.
��(d��ng)![]() �r(sh��)���c(di��n)
�r(sh��)���c(di��n)![]() �ڙE�A
�ڙE�A![]() �⣬���M(m��n)���}��.
�⣬���M(m��n)���}��.
����ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() .
.
��(li��n)��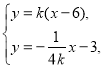 ���
���![]() .
.
����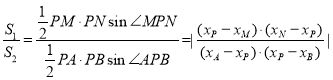
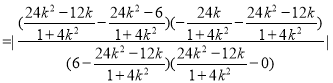
![]()
![]()
![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() ��
��![]() .
.
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����(d��ng)![]() ��
��![]() �r(sh��).
�r(sh��).
����![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ��
��![]() ��
��![]() �������C��
�������C��![]() ��
��
����(du��)�����![]() ������
������![]() ������������(sh��)��(sh��)t�����ֵ.
������������(sh��)��(sh��)t�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������Դ��܇(ch��)�Ĵ����(l��i)�ˣ�2018��3��5�����磬��ˏ�(qi��ng)����������������(b��o)��r(sh��)��ʾ��������Դ��܇(ch��)܇(ch��)�vُ(g��u)�ö���(y��u)�����������L(zh��ng)���꣬��2018��1��1����2020��12��31�գ���(du��)ُ(g��u)�õ�����Դ��܇(ch��)����܇(ch��)�vُ(g��u)�ö�.ij��Ӌ(j��)����2018��5��ُ(g��u)�I(m��i)һ�vijƷ������Դ��܇(ch��)�����Į�(d��ng)?sh��)�ԓƷ���N(xi��o)�۾W(w��ng)վ�˽��˽��傀(g��)�µČ�(sh��)�H�N(xi��o)�����±���
�·� | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
�·ݾ�̖(h��o) | 1 | 2 | 3 | 4 | 5 |
�N(xi��o)�����f(w��n)���� | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
��1����(j��ng)���������þ�(xi��n)�Իؚwģ�͔M�Ϯ�(d��ng)?sh��)�ԓƷ������Դ���?ch��)��(sh��)�H�N(xi��o)��![]() ���f(w��n)�v���c�·ݾ�̖(h��o)
���f(w��n)�v���c�·ݾ�̖(h��o)![]() ֮�g�����P(gu��n)�P(gu��n)ϵ.Ո(q��ng)����С���˷���
֮�g�����P(gu��n)�P(gu��n)ϵ.Ո(q��ng)����С���˷���![]() �P(gu��n)��
�P(gu��n)��![]() �ľ�(xi��n)�Իؚw����
�ľ�(xi��n)�Իؚw����![]() �����A(y��)�y(c��)2018��5�·ݮ�(d��ng)?sh��)�ԓƷ������Դ���?ch��)���N(xi��o)����
�����A(y��)�y(c��)2018��5�·ݮ�(d��ng)?sh��)�ԓƷ������Դ���?ch��)���N(xi��o)����
��2��2018��6��12�գ�����ؔ(c��i)���͵ط�ؔ(c��i)��������(j��)����Դ��܇(ch��)������m(x��)����̣�����Դ��܇(ch��)������m(x��)�������ָ��Փ������Դ��܇(ch��)���b��ȼ�ϻ�늳����܉��ṩ�o܇(ch��)�ܵ����h(yu��n)��̣���(du��)ُ(g��u)܇(ch��)�a(b��)�N�M(j��n)����һ݆�{(di��o)��.��֪ij��?c��i)Mُ(g��u)�I(m��i)����Դ��܇(ch��)�����M(f��i)Ⱥ�wʮ������ij�{(di��o)�ЙC(j��)��(g��u)��(du��)���е�200�����M(f��i)�ߵ�ُ(g��u)܇(ch��)�a(b��)�N���~�������A(y��)��ֵ�M(j��n)����һ��(g��)����{(di��o)�飬�õ�����һ���l��(sh��)����
�a(b��)�N���~�A(y��)��ֵ�^(q��)�g���f(w��n)Ԫ�� |
|
|
|
|
|
|
�l��(sh��) | 20 | 60 | 60 | 30 | 20 | 10 |
��i�����@200λ�Mُ(g��u)�I(m��i)����Դ��܇(ch��)�����M(f��i)�ߌ�(du��)�a(b��)�N���~�������A(y��)��ֵ![]() �ķ���
�ķ���![]() ����λ��(sh��)�Ĺ�Ӌ(j��)ֵ��ͬһ�^(q��)�g���A(y��)��ֵ����ԓ�^(q��)�g�����c(di��n)ֵ���棬��Ӌ(j��)ֵ���_��0.1����
����λ��(sh��)�Ĺ�Ӌ(j��)ֵ��ͬһ�^(q��)�g���A(y��)��ֵ����ԓ�^(q��)�g�����c(di��n)ֵ���棬��Ӌ(j��)ֵ���_��0.1����
��ii�����l��ҕ����ʣ��F(xi��n)���S�C(j��)��ӷ�����ԓ�^(q��)�Mُ(g��u)�I(m��i)����Դ��܇(ch��)���������M(f��i)�����S�C(j��)��ȡ3�ˣ�ӛ����ȡ��3���Ќ�(du��)�a(b��)�N���~�������A(y��)��ֵ������3�f(w��n)Ԫ���˔�(sh��)��![]() ����
����![]() �ķֲ��м���(sh��)�W(xu��)����
�ķֲ��м���(sh��)�W(xu��)����![]() .
.
�����ٻؚwֱ��(xi��n)��б�ʺͽؾ����С���˹�Ӌ(j��)��ʽ�քe�飺 ��
��![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() �������Ă�(g��)�Y(ji��)Փ��
�������Ă�(g��)�Y(ji��)Փ��
��![]() ��ż����(sh��)��
��ż����(sh��)��
��![]() ����С�����ڞ�
����С�����ڞ�![]() ��
��
��![]() ����Сֵ��0��
����Сֵ��0��
��![]() ��
��![]() ����3��(g��)���c(di��n)
����3��(g��)���c(di��n)
�����������_�Y(ji��)Փ�ľ�̖(h��o)�ǣ� ��
A.�٢�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����������![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ߅��һ�c(di��n)��
߅��һ�c(di��n)��![]() ��
��![]() .
.

��1���C����ƽ��![]() ƽ��
ƽ��![]() .
.
��2����![]() ��ԇ��(w��n)��
��ԇ��(w��n)��![]() �Ƿ��cƽ��
�Ƿ��cƽ��![]() ƽ�У���ƽ�У��������F
ƽ�У���ƽ�У��������F![]() ���w�e������ƽ�У�Ո(q��ng)�f(shu��)������.
���w�e������ƽ�У�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ij���^(q��)��һ��(g��)��![]() ��A�ģ��돽��
��A�ģ��돽��![]() �ĈA�΅^(q��)��·
�ĈA�΅^(q��)��·![]() ��
��![]() ��
��![]() �ǣ��Ҿ��;��^(q��)߅�����У��F(xi��n)Ҫ��һ�l�c���^(q��)���е��^(gu��n)��ľ����
�ǣ��Ҿ��;��^(q��)߅�����У��F(xi��n)Ҫ��һ�l�c���^(q��)���е��^(gu��n)��ľ����![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �ϣ�����ľ����
�ϣ�����ľ����![]() �c��·
�c��·![]() ��
��![]() ���ɵ����ǵ؉K
���ɵ����ǵ؉K![]() .
.

��1��������ľ����![]() �c��·
�c��·![]() ��
��![]() ���ɵ����ǵ؉K
���ɵ����ǵ؉K![]() ��e����Сֵ��
��e����Сֵ��
��2�������^(q��)����![]() �cľ����
�cľ����![]() ���B��(xi��n)��
���B��(xi��n)��![]() .
.
�ٌ�ľ����![]() ���L(zh��ng)�ȱ�ʾ��
���L(zh��ng)�ȱ�ʾ��![]() �ĺ���(sh��)����ָ�����x��
�ĺ���(sh��)����ָ�����x��
�����ľ����![]() ���L(zh��ng)����Сֵ.
���L(zh��ng)����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���錍(sh��)�F(xi��n)��(gu��)��(j��ng)��(j��)�������������İl(f��)չ��(zh��n)��Ŀ��(bi��o)����(gu��)�ҼӴ��˷�ؚ����(ji��n)�����ȣ�ij�^(q��)��2015����ǰ�����Óؚ�ʣ�Óؚ�đ�(h��)��(sh��)ռ��(d��ng)��ؚ����(h��)����(sh��)�ıȣ���70����2015���_(k��i)ʼȫ�挍(sh��)ʩ������(zh��n)��ؚ�����ߺ�ؚЧ�����@��ߣ�����2019��Ȍ�(sh��)ʩ�ķ�ؚ�(xi��ng)Ŀ�����(xi��ng)Ŀ���ӑ�(h��)��(sh��)ռ�ȣ����ӑ�(h��)��(sh��)ռ2019��ؚ������(h��)��(sh��)�ıȣ���ԓ�(xi��ng)Ŀ��Óؚ��Ҋ(ji��n)�±���
��(sh��)ʩ�(xi��ng)Ŀ | �Nֲ�I(y��) | �B(y��ng)ֳ�I(y��) | ���S(ch��ng)�͘I(y��) |
����ռ��(h��)�� | 45�� | 45�� | 10�� |
Óؚ�� | 96�� | 96�� | 90�� |
��ô2019�����Óؚ���nj�(sh��)ʩ������(zh��n)��ؚ������ǰ�����Óؚ�ʵģ� ����.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪![]() �钁�タ(xi��n)
�钁�タ(xi��n)![]() ��һ�c(di��n)��б�ʷքe��
��һ�c(di��n)��б�ʷքe��![]() ��
��![]()
![]() ��ֱ��(xi��n)PA��PB�քe�����タ(xi��n)���c(di��n)A��B�����c�c(di��n)P�غϣ�.
��ֱ��(xi��n)PA��PB�քe�����タ(xi��n)���c(di��n)A��B�����c�c(di��n)P�غϣ�.

��1���C����ֱ��(xi��n)AB��б�ʞ鶨ֵ��
��2������ABP�ă�(n��i)�ЈA�돽��![]() .
.
��i�����ABP�����L(zh��ng)����k��ʾ����
��ii����ֱ��(xi��n)AB�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ������(bi��o)ԭ�c(di��n)���E�A
������(bi��o)ԭ�c(di��n)���E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���x���ʞ�
���x���ʞ�![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]()
![]() �c
�c![]() �ཻ��
�ཻ��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() �龀(xi��n)��
�龀(xi��n)��![]() �����c(di��n).
�����c(di��n).
��1����(d��ng)![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() �r(sh��)����ֱ��(xi��n)
�r(sh��)����ֱ��(xi��n)![]() �ķ��̣�
�ķ��̣�
��2��ԇ̽����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ�������ڣ�����c(di��n)
�鶨ֵ�������ڣ�����c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com