
【題目】已知直三棱柱ABC﹣A1B1C1的6個頂點都在球O的球面上,若AB=3,AC=3,∠BAC=120°,AA1=8,則球O的表面積為( )
A.25πB.![]() πC.100πD.
πC.100πD.![]() π
π
科目:高中數學 來源: 題型:
【題目】某蛋糕店每天制作生日蛋糕若干個,每個生日蛋糕成本為50元,每個蛋糕的售價為100元,如果當天賣不完,剩余的蛋糕作垃圾處理.現搜集并整理了100天生日蛋糕的日需求量(單位:個),得到如圖所示的柱狀圖.100天記錄的各需求量的頻率作為每天各需求量發生的概率.

(1)若該蛋糕店某一天制作生日蛋糕17個,設當天的需求量為![]() ,則當天的利潤
,則當天的利潤![]() (單位:元)是多少?
(單位:元)是多少?
(2)若蛋糕店一天制作17個生日蛋糕.
①求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() 的函數解析式;
的函數解析式;
②求當天的利潤不低于600圓的概率.
(3)若蛋糕店計劃一天制作16個或17個生日蛋糕,請你以蛋糕店一天利潤的平均值作為決策依據,應該制作16個還是17個生日蛋糕?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小學六年級學生的進行一分鐘跳繩檢測,現一班二班各有50人,根據檢測結果繪出了一班的頻數分布表和二班的頻率分布直方圖.
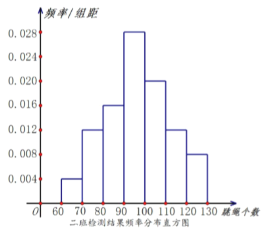
一班檢測結果頻數分布表:
跳繩個數區間 |
|
|
|
|
|
頻數 | 7 | 13 | 20 | 8 | 2 |
(1)根據給出的圖表估計一班和二班檢測結果的中位數(結果保留兩位小數);
(2)跳繩個數不小于100個為優秀,填寫下面2×2列聯表,并根據列聯表判斷是否有95%的把握認為檢測結果是否優秀與班級有關.
一班 | 二班 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
參考公式及數據: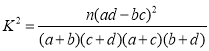 ,
,
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 1(a>b>0)的離心率為
1(a>b>0)的離心率為![]() ,O是坐標原點,點A,B分別為橢圓C的左右頂點,|AB|=4
,O是坐標原點,點A,B分別為橢圓C的左右頂點,|AB|=4![]() .
.
(1)求橢圓C的標準方程.
(2)若P是橢圓C上異于A,B的一點,直線l交橢圓C于M,N兩點,AP∥OM,BP∥ON,則△OMN的面積是否為定值?若是,求出定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障全國第四次經濟普查順利進行,國家統計局從東部選擇江蘇,從中部選擇河北、湖北,從西部選擇寧夏,從直轄市中選擇重慶作為國家綜合試點地區,然后再逐級確定普查區域,直到基層的普查小區,在普查過程中首先要進行宣傳培訓,然后確定對象,最后入戶登記,由于種種情況可能會導致入戶登記不夠順利,這為正式普查提供了寶貴的試點經驗,在某普查小區,共有50家企事業單位,150家個體經營戶,普查情況如下表所示:
普查對象類別 | 順利 | 不順利 | 合計 |
企事業單位 | 40 | 10 | 50 |
個體經營戶 | 100 | 50 | 150 |
合計 | 140 | 60 | 200 |
(1)寫出選擇5個國家綜合試點地區采用的抽樣方法;
(2)根據列聯表判斷是否有![]() 的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
(3)以該小區的個體經營戶為樣本,頻率作為概率,從全國個體經營戶中隨機選擇3家作為普查對象,入戶登記順利的對象數記為![]() ,寫出
,寫出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地有A,B、C、D四人先后感染了新型冠狀病毒,其中只有A到過疫區,B肯定是受A感染的,對于C,因為難以判定他是受A還是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同樣也假設D受A、B和C感染的概率都是
,同樣也假設D受A、B和C感染的概率都是![]() .在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
.在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中把三角形的田稱為“圭田”,把直角梯形的田稱為“邪田”,稱底是“廣”,稱高是“正從”,“步”是丈量土地的單位.現有一邪田,廣分別為十步和二十步,正從為十步,其內有一塊廣為八步,正從為五步的圭田.若在邪田內隨機種植一株茶樹,求該株茶樹恰好種在圭田內的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com