
【題目】已知四邊形![]() 是矩形,
是矩形,![]() ,將
,將![]() 沿著對角線AC翻折,得到
沿著對角線AC翻折,得到![]() ,設頂點
,設頂點![]() 在平面
在平面![]() 上的投影為O.
上的投影為O.
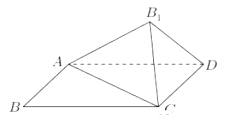
(1)若點O恰好落在邊AD上,①求證:![]() 平面
平面![]() ;②若
;②若![]() ,
,![]() ,當BC取到最小值時,求k的值;
,當BC取到最小值時,求k的值;
(2)當![]() 時,若點O恰好落在
時,若點O恰好落在![]() 的內部(不包括邊界),求二面角
的內部(不包括邊界),求二面角![]() 的余弦值的取值范圍.
的余弦值的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由面面垂直的判定定理得平面
由面面垂直的判定定理得平面![]() 平面ACD,從而
平面ACD,從而![]() ,由線面垂直得
,由線面垂直得![]() ,由矩形性質得
,由矩形性質得![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
![]() 作矩形ABMN,使得
作矩形ABMN,使得![]() 在MN上,設
在MN上,設![]() ,
,![]() ,求出y,利用基本不等式,即可求出當BC取到最小值時,k的值;
,求出y,利用基本不等式,即可求出當BC取到最小值時,k的值;
![]() 作
作![]() ,交AC于E,交AD于F,當點O恰好落在
,交AC于E,交AD于F,當點O恰好落在![]() 的內部
的內部![]() 不包括邊界
不包括邊界![]() ,點O恰好在線段EF上,
,點O恰好在線段EF上,![]() 為二面角
為二面角![]() 的平面角,由此能求出二面角
的平面角,由此能求出二面角![]() 的余弦值的取值范圍.
的余弦值的取值范圍.
![]() 證明:
證明:![]() 點
點![]() 在平面ABCD上的射影為O,點O恰好落在邊AD上,
在平面ABCD上的射影為O,點O恰好落在邊AD上,
![]() 平面
平面![]() 平面ACD,又
平面ACD,又![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,
![]() 平面
平面![]() .
.
![]() 作矩形ADMN,使得
作矩形ADMN,使得![]() 在MN上,
在MN上,
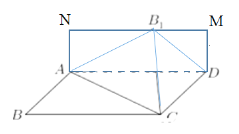
設![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,![]() ∽
∽![]() ,
,
![]() ,
,
在Rt![]() 中
中
![]() ,
,
當且僅當![]() 時取等號,y有最小值,
時取等號,y有最小值,![]() ;
;
![]() 作
作![]() ,交AC于E,交AD于F,
,交AC于E,交AD于F,
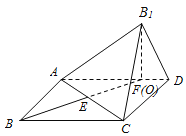
當點O恰好落在![]() 的內部
的內部![]() 不包括邊界
不包括邊界![]() ,點O恰好在線段EF上,
,點O恰好在線段EF上,
又![]() ,
,![]() ,
,
![]() 為二面角
為二面角![]() 的平面角,
的平面角,
當![]() 時,由
時,由![]() ,可得
,可得![]() ,且
,且![]() ,
,
![]() ,
,
故二面角![]() 的余弦值的取值范圍為
的余弦值的取值范圍為![]()


科目:高中數學 來源: 題型:
【題目】以下四個關于圓錐曲線的命題中
①設A.B為兩個定點,k為非零常數,![]() ,則動點P的軌跡為雙曲線;
,則動點P的軌跡為雙曲線;
②曲線![]() 表示焦點在y軸上的橢圓,則
表示焦點在y軸上的橢圓,則![]() ;
;
③方程![]() 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
④雙曲![]() 與橢圓
與橢圓![]() 有相同的焦點.
有相同的焦點.
其中真命題的序號( )
A.②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高二年級舉行一次演講賽共有10位同學參賽,其中一班有3位,二班有2位,其它班有5位,若采用抽簽的方式確定他們的演講順序,則一班有3位同學恰好被排在一起(指演講序號相連),而二班的2位同學沒有被排在一起的概率為:( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點F為圓C:
的焦點F為圓C:![]() 的圓心.
的圓心.
![]() 求拋物線的方程與其準線方程;
求拋物線的方程與其準線方程;
![]() 直線l與圓C相切,交拋物線于A,B兩點;
直線l與圓C相切,交拋物線于A,B兩點;
![]() 若線段AB中點的縱坐標為
若線段AB中點的縱坐標為![]() ,求直線l的方程;
,求直線l的方程;
![]() 求
求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
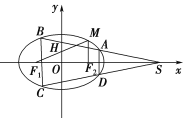
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面ABCD是正方形,平面
中,底面ABCD是正方形,平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面ABCD.
平面ABCD.
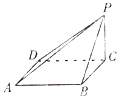
![]() Ⅰ
Ⅰ![]() 證明:
證明:![]() 平面ABCD;
平面ABCD;
![]() Ⅱ
Ⅱ![]() 若二面角
若二面角![]() 的大小為
的大小為![]() ,求PB與平面PAD所成角的大小.
,求PB與平面PAD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓C過點
,且橢圓C過點![]() .
.
(1)求橢圓C的標準方程;
(2)過橢圓C的右焦點的直線l與橢圓C交于A、B兩點,且與圓:![]() 交于E、F兩點,求
交于E、F兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com