
【題目】已知點(1, ![]() )是函數(shù)f(x)=
)是函數(shù)f(x)= ![]() ax(a>0,a≠1)圖象上一點,等比數(shù)列{an}的前n項和為c﹣f(n).數(shù)列{bn}(bn>0)的首項為2c,前n項和滿足
ax(a>0,a≠1)圖象上一點,等比數(shù)列{an}的前n項和為c﹣f(n).數(shù)列{bn}(bn>0)的首項為2c,前n項和滿足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求數(shù)列{an}的通項公式;
+1(n≥2). (Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)若數(shù)列{ ![]() }的前n項和為Tn , 問使Tn>
}的前n項和為Tn , 問使Tn> ![]() 的最小正整數(shù)n是多少?
的最小正整數(shù)n是多少?
【答案】(Ⅰ)解: ![]() .∴
.∴ ![]() , ∵
, ∵ ![]() ,則等比數(shù)列{an}的前n項和為c﹣
,則等比數(shù)列{an}的前n項和為c﹣ ![]()
![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]()
由{an}為等比數(shù)列,得公比q= ![]()
∴ 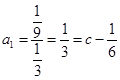 ,則c=
,則c= ![]() ,a
,a ![]()
∴ ![]()
(Ⅱ):由b1=2c=1,得s1=1
n≥2時, ![]() ,則
,則 ![]() 是首項為1,公差為1的等差數(shù)列.
是首項為1,公差為1的等差數(shù)列.
∴ ![]() ,
, ![]() (n∈N+)
(n∈N+)
則 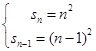 (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2).
當n=1時,b1=1滿足上式
∴ ![]()
∵ ![]() =
= ![]() =
= ![]()
∴Tn= ![]() =
= ![]() =
= ![]()
由Tn= ![]() ,得n
,得n ![]() ,則最小正整數(shù)n為59
,則最小正整數(shù)n為59
【解析】(Ⅰ)由已知求得a, ![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]() ,得公比q=
,得公比q= ![]() ,即可寫出通項;(Ⅱ)可得
,即可寫出通項;(Ⅱ)可得 ![]() 是首項為1,公差為1的等差數(shù)列.由
是首項為1,公差為1的等差數(shù)列.由 ![]() (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2). ![]() =
= ![]() =
= ![]() ,累加求得Tn=
,累加求得Tn= ![]() ,得n
,得n ![]() ,即可得最小正整數(shù)n.
,即可得最小正整數(shù)n.


 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知{an}是一個等差數(shù)列且a2+a8=﹣4,a6=2
(1)求{an}的通項公式;
(2)求{an}的前n項和Sn的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
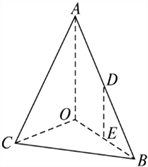
【題目】如圖,在三棱錐![]() 中,
中, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.(19)
的中點.(19)
(I)求![]() 到平面
到平面![]() 的距離;
的距離;
(II)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() ∥平面
∥平面![]() ,若存在,試確定
,若存在,試確定![]() 的位置,并證明此點滿足要求;若不存在,請說明理由.
的位置,并證明此點滿足要求;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}是等差數(shù)列,{bn}是等比數(shù)列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通項公式;
(Ⅱ)設cn=an+bn , 求數(shù)列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義在R上的偶函數(shù)f(x)滿足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是減函數(shù),若α,β是銳角三角形的兩個內(nèi)角,則( )
,且f(x)在[﹣3,﹣2]上是減函數(shù),若α,β是銳角三角形的兩個內(nèi)角,則( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以橢圓C的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0),設圓T與橢圓C交于點M與點N.
,以橢圓C的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0),設圓T與橢圓C交于點M與點N. 
(1)求橢圓C的方程;
(2)求 ![]()
![]() 的最小值;
的最小值;
(3)設點P是橢圓C上異于M,N的任意一點,且直線MP,NP分別與x軸交于點R,S,O為坐標原點,求證:|OR||OS|是定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】觀察以下三個等式: sin215°﹣sin245°+sin15°cos45°=﹣ ![]() ,
,
sin220°﹣sin250°+sin20°cos50°=﹣ ![]() ,
,
sin230°﹣sin260°+sin30°cos60°=﹣ ![]() ;
;
猜想出一個反映一般規(guī)律的等式: .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com