
函數(shù)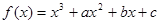 ,過曲線
,過曲線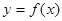 上的點(diǎn)
上的點(diǎn)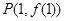 的切線方程為
的切線方程為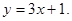 .
.
(1)若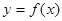 在
在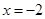 時(shí)有極值,求
時(shí)有極值,求 的表達(dá)式;
的表達(dá)式;
(2)在(1)的條件下,求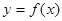 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函數(shù)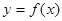 在區(qū)間[-2,1]上單調(diào)遞增,求實(shí)數(shù)b的取值范圍.
在區(qū)間[-2,1]上單調(diào)遞增,求實(shí)數(shù)b的取值范圍.
(1) ;(2)13;(3)
;(2)13;(3)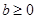 .
.
解析試題分析:(1)題目條件給出了關(guān)于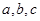 的兩組關(guān)系,第一問中又給出了一組關(guān)系,所以在第一問很容易就能將表達(dá)式求出;(2)我們求解無(wú)參函數(shù)在定區(qū)間上的最大值,只需求導(dǎo)看
的兩組關(guān)系,第一問中又給出了一組關(guān)系,所以在第一問很容易就能將表達(dá)式求出;(2)我們求解無(wú)參函數(shù)在定區(qū)間上的最大值,只需求導(dǎo)看 在
在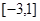 上的單調(diào)性,然后找到極小值就是最小值,最大值通過比較端點(diǎn)值即可判斷出;(3)考查函數(shù)單調(diào)性的問題,我們可以將其轉(zhuǎn)化為不等式恒成立問題,轉(zhuǎn)化之后的不等式是比較常見的二次不等式恒成立,一般碰到這種問題我們采取分離參數(shù)的方法將參數(shù)分到一邊,求出另一邊的最值即可,另一邊的函數(shù)是常見的對(duì)勾函數(shù),在這里區(qū)間給的比較好,可以讓我們用基本不等式解出最大值,然后參數(shù)大于最大值即可.
上的單調(diào)性,然后找到極小值就是最小值,最大值通過比較端點(diǎn)值即可判斷出;(3)考查函數(shù)單調(diào)性的問題,我們可以將其轉(zhuǎn)化為不等式恒成立問題,轉(zhuǎn)化之后的不等式是比較常見的二次不等式恒成立,一般碰到這種問題我們采取分離參數(shù)的方法將參數(shù)分到一邊,求出另一邊的最值即可,另一邊的函數(shù)是常見的對(duì)勾函數(shù),在這里區(qū)間給的比較好,可以讓我們用基本不等式解出最大值,然后參數(shù)大于最大值即可.
試題解析:(1)由 得
得 ,過
,過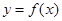 上點(diǎn)
上點(diǎn)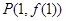 的切線方
的切線方
程為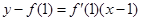 ,即
,即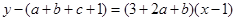 .而過
.而過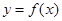 上點(diǎn)
上點(diǎn)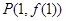 的切
的切
線方程為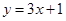 ,故
,故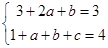 即
即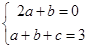 ,∵
,∵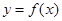 在
在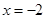 處有極值,
處有極值,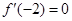 ,
,
∴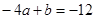 ,聯(lián)立解得
,聯(lián)立解得 .∴
.∴ .
.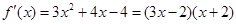 ,令
,令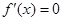 得
得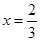 或
或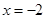 ,列下表:
,列下表: