
【題目】【2017廣東佛山二模】已知橢圓![]() :
: ![]() (
(![]() )的焦距為4,左、右焦點(diǎn)分別為
)的焦距為4,左、右焦點(diǎn)分別為![]() 、
、![]() ,且
,且![]() 與拋物線
與拋物線![]() :
: ![]() 的交點(diǎn)所在的直線經(jīng)過
的交點(diǎn)所在的直線經(jīng)過![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),與拋物線
兩點(diǎn),與拋物線![]() 無公共點(diǎn),求
無公共點(diǎn),求![]() 的面積的取值范圍.
的面積的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  .
.
【解析】試題分析:(1)先根據(jù)焦距確定焦點(diǎn)坐標(biāo),再根據(jù)對稱性得![]() 與拋物線
與拋物線![]() :
: ![]() 的交點(diǎn)所在的直線為
的交點(diǎn)所在的直線為![]() ,即得一個交點(diǎn)為
,即得一個交點(diǎn)為![]() ,代入橢圓方程,結(jié)合
,代入橢圓方程,結(jié)合![]() 可解得
可解得![]() ,
, ![]() ;(2)先設(shè)直線
;(2)先設(shè)直線![]() :
: ![]() ,由直線
,由直線![]() 與拋物線
與拋物線![]() 無公共點(diǎn),利用判別式小于零得
無公共點(diǎn),利用判別式小于零得![]() .由弦長公式可求底邊AB長,利用點(diǎn)
.由弦長公式可求底邊AB長,利用點(diǎn)![]() 到直線
到直線![]() 距離可得高,代入面積公式可得
距離可得高,代入面積公式可得![]() ,根據(jù)對勾函數(shù)確定其值域.
,根據(jù)對勾函數(shù)確定其值域.
試題解析:(Ⅰ)依題意得![]() ,則
,則![]() ,
, ![]() .
.
所以橢圓![]() 與拋物線
與拋物線![]() 的一個交點(diǎn)為
的一個交點(diǎn)為![]() ,
,
于是![]()
![]() ,從而
,從而![]() .
.
又![]() ,解得
,解得![]()
所以橢圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)依題意,直線![]() 的斜率不為0,設(shè)直線
的斜率不為0,設(shè)直線![]() :
: ![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,由
,由![]() 得
得![]() .
.
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
設(shè)![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
,
所以![]()
![]()
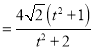 ,
,
![]() 到直線
到直線![]() 距離
距離![]() ,
,
故![]()
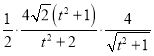
![]() ,
,
令![]() ,則
,則![]()

 ,
,
所以三邊形![]() 的面積的取值范圍為
的面積的取值范圍為 .
.


 小學(xué)生10分鐘口算測試100分系列答案
小學(xué)生10分鐘口算測試100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓M的圓心為M(﹣1,2),直線y=x+4被圓M截得的弦長為 ![]() ,點(diǎn)P在直線l:y=x﹣1上.
,點(diǎn)P在直線l:y=x﹣1上.
(1)求圓M的標(biāo)準(zhǔn)方程;
(2)設(shè)點(diǎn)Q在圓M上,且滿足 ![]() =4
=4 ![]() ,求點(diǎn)P的坐標(biāo);
,求點(diǎn)P的坐標(biāo);
(3)設(shè)半徑為5的圓N與圓M相離,過點(diǎn)P分別作圓M與圓N的切線,切點(diǎn)分別為A,B,若對任意的點(diǎn)P,都有PA=PB成立,求圓心N的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】福利彩票“雙色球”中紅球的號碼可以從01,02,03,…,32,33這33個二位號碼中選取,小明利用如圖所示的隨機(jī)數(shù)表選取紅色球的6個號碼,選取方法是從第1行第9列和第10列的數(shù)字開始從左到右依次選取兩個數(shù)字,則第四個被選中的紅色球號碼為( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】實驗杯足球賽采用七人制淘汰賽規(guī)則,某場比賽中一班與二班在常規(guī)時間內(nèi)戰(zhàn)平,直接進(jìn)入點(diǎn)球決勝環(huán)節(jié),在點(diǎn)球決勝環(huán)節(jié)中,雙方首先輪流罰點(diǎn)球三輪,罰中更多點(diǎn)球的球隊獲勝;若雙方在三輪罰球中未分勝負(fù),則需要進(jìn)行一對一的點(diǎn)球決勝,即雙方各派處一名隊員罰點(diǎn)球,直至分出勝負(fù);在前三輪罰球中,若某一時刻勝負(fù)已分,尚未出場的隊員無需出場罰球(例如一班在先罰球的情況下,一班前兩輪均命中,二班前兩輪未能命中,則一班、二班的第三位同學(xué)無需出場).由于一班同學(xué)平時踢球熱情較高,每位隊員罰點(diǎn)球的命中率都能達(dá)到0.8,而二班隊員的點(diǎn)球命中串只有0.5,比賽時通過抽簽決定一班在每一輪都先罰球.
(1)定義事件![]() 為“一班第三位同學(xué)沒能出場罰球”,求事件
為“一班第三位同學(xué)沒能出場罰球”,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(2)若兩隊在前三輪點(diǎn)球結(jié)束后打平,則進(jìn)入一對一點(diǎn)球決勝,一對一球決勝由沒有在之前點(diǎn)球大戰(zhàn)中出場過的隊員主罰點(diǎn)球,若在一對一點(diǎn)球決勝的某一輪中,某對隊員射入點(diǎn)球且另一隊員未能射入,則比賽結(jié)束;若兩名隊員均射入或者均射失點(diǎn)球,則進(jìn)行下一輪比賽. 若直至雙方場上每名隊員都已經(jīng)出場罰球,則比賽亦結(jié)束,雙方通過抽簽決定勝負(fù),本場比賽中若已知雙方在點(diǎn)球大戰(zhàn),以隨機(jī)變量![]() 記錄雙方進(jìn)行一對一點(diǎn)球決勝的輪數(shù),求
記錄雙方進(jìn)行一對一點(diǎn)球決勝的輪數(shù),求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】極坐標(biāo)系的極點(diǎn)為直角坐標(biāo)系的原點(diǎn),極軸為x軸的正半軸,兩種坐標(biāo)系中的長度單位相同,已知曲線C的極坐標(biāo)方程為ρ=2(cosθ+sinθ).
(1)求C的直角坐標(biāo)方程;
(2)直線l: 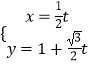 為參數(shù))與曲線C交于A,B兩點(diǎn),與y軸交于E,求|EA|+|EB|的值.
為參數(shù))與曲線C交于A,B兩點(diǎn),與y軸交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合A={x|y= ![]() },B={x|x2﹣2x+1﹣m2≤0}.
},B={x|x2﹣2x+1﹣m2≤0}.
(1)若m=3,求A∩B;
(2)若m>0,AB,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)當(dāng)a=1時,解不等式f(x)≥g(x);
(2)記函數(shù)f(x)在區(qū)間[0,2]上的最大值為F(a),求F(a)的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的首項a1=a,Sn是數(shù)列{an}的前n項和,且滿足: ![]() =3n2an+
=3n2an+![]() ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若數(shù)列{an}是等差數(shù)列,求a的值;
(2)確定a的取值集合M,使a∈M時,數(shù)列{an}是遞增數(shù)列.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com