
【題目】在數(shù)列{an}中,a1=1,an+1=2an+2n .
(1)設bn= ![]() ,證明:數(shù)列{bn}是等差數(shù)列.
,證明:數(shù)列{bn}是等差數(shù)列.
(2)求數(shù)列{an}的前n項和.
【答案】
(1)證明:∵an+1=2an+2n,∴ ![]() ,
,
∴bn+1﹣bn=1.
∴數(shù)列{bn}是等差數(shù)列,首項為 ![]() =1,公差為1
=1,公差為1
(2)解:由(1)可得:bn=1+(n﹣1)=n,
∴ ![]() ,
,
∴ ![]() ,
,
∴數(shù)列{an}的前n項和Sn=1+2×2+3×22+…+n2n﹣1,
2Sn=2+2×22+3×23+…+(n﹣1)×2n﹣1+n×2n,
∴﹣Sn=1+2+22+…+2n﹣1﹣n×2n= ![]() ﹣n×2n=(1﹣n)×2n﹣1.
﹣n×2n=(1﹣n)×2n﹣1.
∴Sn=(n﹣1)×2n+1
【解析】(1)由an+1=2an+2n , 可得 ![]() ,即bn+1﹣bn=1.即可證明;(2)由(1)可得:bn=1+(n﹣1)=n,
,即bn+1﹣bn=1.即可證明;(2)由(1)可得:bn=1+(n﹣1)=n, ![]() ,再利用“錯位相減法”、等比數(shù)列的前n項和公式即可得出.
,再利用“錯位相減法”、等比數(shù)列的前n項和公式即可得出.
【考點精析】利用等差關系的確定和數(shù)列的前n項和對題目進行判斷即可得到答案,需要熟知如果一個數(shù)列從第2項起,每一項與它的前一項的差等于同一個常數(shù),即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么這個數(shù)列就叫做等差數(shù)列;數(shù)列{an}的前n項和sn與通項an的關系
)那么這個數(shù)列就叫做等差數(shù)列;數(shù)列{an}的前n項和sn與通項an的關系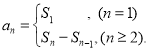 .
.


科目:高中數(shù)學 來源: 題型:
【題目】給定兩個命題,P:對任意實數(shù)x都有ax2+ax+1>0恒成立;Q:關于x的方程x2﹣x+a=0有實數(shù)根;如果P與Q中有且僅有一個為真命題,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知△ABC是斜三角形,內(nèi)角A、B、C所對的邊的長分別為a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面積.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}是一個公差大于0的等差數(shù)列,且滿足![]() ,a2+a7=16
,a2+a7=16
(1)求數(shù)列{an}的通項公式;
(2)數(shù)列{an}和數(shù)列{bn}滿足等式![]() (n∈N*),求數(shù)列{bn}的前n項和Sn.
(n∈N*),求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,設![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數(shù)
的距離的比是常數(shù)![]() ,
,
(1)求點![]() 的軌跡曲線
的軌跡曲線![]() 的方程:
的方程:
(2)過定點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,以
兩點,以![]() 三點(
三點(![]() 為坐標原點)為頂點作平行四邊形
為坐標原點)為頂點作平行四邊形![]() ,若點
,若點![]() 剛好在曲線
剛好在曲線![]() 上,求直線
上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知正方體ABCD﹣A1B1C1D1的棱AA1=2,求: 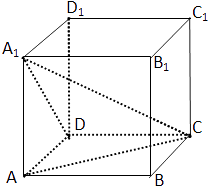
(1)求異面直線A1D與AC所成角的大小;
(2)求四面體A1﹣DCA的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】正四棱錐(底面為正方形,頂點在底面上的射影是底面的中心)S﹣ABCD的底面邊長為2,高為2,E為邊BC的中點,動點P在表面上運動,并且總保持PE⊥AC,則動點P的軌跡的周長為( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,半徑為![]() 的圓形紙板內(nèi)有一個相同圓心的半徑為
的圓形紙板內(nèi)有一個相同圓心的半徑為![]() 的小圓,現(xiàn)將半徑為
的小圓,現(xiàn)將半徑為![]() 的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內(nèi),則硬幣與小圓無公共點的概率為( )
的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內(nèi),則硬幣與小圓無公共點的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)設角A,B,C的對邊依次為a,b,c,若c=2,且△ABC是銳角三角形,求a2+b2的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com