
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,且
,且![]() 是
是![]() 的中點.
的中點.
(Ⅰ)求橢圓的離心率;
(Ⅱ)過點![]() 的直線與橢圓相交于
的直線與橢圓相交于![]() 兩點,
兩點,![]() 都在
都在![]() 軸上方,并且
軸上方,并且![]() 在
在![]() 之間,且
之間,且![]() 到直線
到直線![]() 的距離是
的距離是![]() 到直線
到直線![]() 距離的
距離的![]() 倍.
倍.
①記![]() 的面積分別為
的面積分別為![]() ,求
,求![]() ;
;
②若原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求橢圓方程.
,求橢圓方程.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
試題本題以直線與橢圓的位置關系為背景.第(1)小題設計為求橢圓的離心率,只需利用條件![]() 是
是![]() 的中點,可得
的中點,可得![]() ,從而得
,從而得![]() .第(2)小題中第①題求
.第(2)小題中第①題求![]() ,需要用等積法進行轉化,即
,需要用等積法進行轉化,即![]() .第②題求橢圓方程,設直線
.第②題求橢圓方程,設直線![]() 方程為
方程為![]() .注意到
.注意到![]() ,和原點
,和原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,![]() ,從而可以確定
,從而可以確定![]() ,
,![]() ,
,![]() 的值.
的值.
試題解析:(1)因為![]() 是
是![]() 的中點,所以
的中點,所以![]() ,即
,即![]() ,又
,又![]() 、
、![]() ,
,
所以![]() ,所以
,所以![]() ;
;
(2)①解法一:過![]() 作直線
作直線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,依題意,
,依題意,![]() ,
,
又![]() ,故
,故![]() ,故
,故![]() 是
是![]() 的中點,∴
的中點,∴![]() ,
,
又![]() 是
是![]() 中點,∴
中點,∴![]() ,∴
,∴![]() ;
;
解法二:∵![]() ,∴
,∴![]() ,橢圓方程為
,橢圓方程為![]() ,
,![]() ,
,![]() ,
,
設![]() ,
,![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,即有
上,即有![]() ,
,
![]()
![]()
同理![]() ,
,
又![]() ,故
,故![]() 得
得![]() 是
是![]() 的中點,∴
的中點,∴![]() ,
,
又![]() 是
是![]() 中點,∴
中點,∴![]() ,∴
,∴![]() ;
;
②解法一:設![]() ,則橢圓方程為
,則橢圓方程為![]() ,
,
由①知![]() 是
是![]() 的中點,不妨設
的中點,不妨設![]() ,則
,則![]() ,
,
又![]() 都在橢圓上,即有
都在橢圓上,即有![]()
 即
即![]()

兩式相減得:![]() ,解得
,解得![]() ,
,
可得![]() ,故直線
,故直線![]() 的斜率為
的斜率為 ,
,
直線![]() 的方程為
的方程為![]() ,即
,即![]()
原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
依題意![]() ,解得
,解得![]() ,故橢圓方程為
,故橢圓方程為![]() .
.
解法二:設![]() ,則橢圓方程為
,則橢圓方程為![]() ,
,
由①知![]() 是
是![]() 的中點,故
的中點,故![]() ,
,
直線![]() 的斜率顯然存在,不妨設為
的斜率顯然存在,不妨設為![]() ,故其方程為
,故其方程為![]() ,與橢圓聯立,并消去
,與橢圓聯立,并消去![]() 得:
得:![]() ,整理得:
,整理得:![]() ,(*)
,(*)
設![]() ,
,![]() ,依題意:
,依題意:![]()
 ]
]
由![]()
 解得:
解得:![]()

所以![]() ,解之得:
,解之得:![]() ,即
,即![]() .
.
直線![]() 的方程為
的方程為![]() ,即
,即![]()
原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
依題意![]() ,解得
,解得![]() ,故橢圓方程為
,故橢圓方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】點外賣現已成為上班族解決午餐問題的一種流行趨勢.某配餐店為擴大品牌影響力,決定對新顧客實行讓利促銷,規定:凡點餐的新顧客均可獲贈10元或者16元代金券一張,中獎率分別為![]() 和
和![]() ,每人限點一餐,且100%中獎.現有A公司甲、乙、丙、丁四位員工決定點餐試吃.
,每人限點一餐,且100%中獎.現有A公司甲、乙、丙、丁四位員工決定點餐試吃.
(Ⅰ) 求這四人中至多一人抽到16元代金券的概率;
(Ⅱ) 這四人中抽到10元、16元代金券的人數分別用![]() 、
、![]() 表示,記
表示,記![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“五一”期間,甲乙兩個商場分別開展促銷活動.
(Ⅰ)甲商場的規則是:凡購物滿100元,可抽獎一次,從裝有大小、形狀相同的4個白球、4個黑球的袋中摸出4個球,中獎情況如下表:
摸出的結果 | 獲得獎金(單位:元) |
4個白球或4個黑球 | 200 |
3個白球1個黑球或3個黑球1個白球 | 20 |
2個黑球2個白球 | 10 |
記![]() 為抽獎一次獲得的獎金,求
為抽獎一次獲得的獎金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商場的規則是:凡購物滿100元,可抽獎10次.其中,第![]() 次抽獎方法是:從編號為
次抽獎方法是:從編號為![]() 的袋中(裝有大小、形狀相同的
的袋中(裝有大小、形狀相同的![]() 個白球和
個白球和![]() 個黑球)摸出
個黑球)摸出![]() 個球,若該次摸出的
個球,若該次摸出的![]() 個球顏色都相同,則可獲得獎金
個球顏色都相同,則可獲得獎金![]() 元;記第
元;記第![]() 次獲獎概率
次獲獎概率![]() .設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
.設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
①求證:![]() ;
;
②若某顧客購買120元的商品,不考慮其它因素,從獲得獎金的期望分析,他應該選擇哪一家商場?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】莖葉圖記錄了甲,乙兩組各四名同學單位時間內引體向上的次數,乙組記錄中有一個數據模糊,無法確認,在圖中以X表示.
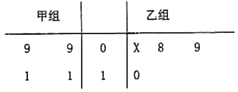
(1)如果X=8,求乙組同學單位時間內引體向上次數的平均數和方差;
(2)如果X=9,分別從甲,乙兩組中隨機選取一名同學,求這兩名同學單位時間內引體向上次數和為19的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(Ⅰ)求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題:
①“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
②“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 上為增函數”的充分不必要條件
上為增函數”的充分不必要條件
③若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
④對于命題![]() :
:![]() ,
,![]() ,則
,則![]() 為:
為:![]() ,
,![]()
其中真命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com