
已知一個關于正整數(shù)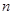 的命題
的命題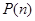 滿足“若
滿足“若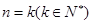 時命題
時命題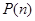 成立,則
成立,則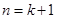 時命題
時命題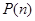 也成立”.有下列判斷:
也成立”.有下列判斷:
(1)當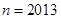 時命題
時命題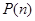 不成立,則
不成立,則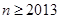 時命題
時命題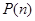 不成立;
不成立;
(2)當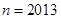 時命題
時命題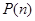 不成立,則
不成立,則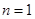 時命題
時命題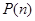 不成立;
不成立;
(3)當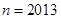 時命題
時命題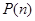 成立,則
成立,則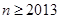 時命題
時命題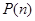 成立;
成立;
(4)當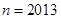 時命題
時命題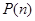 成立,則
成立,則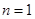 時命題
時命題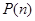 成立.
成立.
其中正確判斷的序號是 .(寫出所有正確判斷的序號)
 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
已知{![]() }(
}(![]() 是正整數(shù))是首項是
是正整數(shù))是首項是![]() ,公比是
,公比是![]() 的等比數(shù)列。
的等比數(shù)列。
(1)求和:①![]() ②
②![]()
(2)由(1)的結果歸納概括出關于正整數(shù)![]() 的一個結論;
的一個結論;
(3)設![]() 是等比數(shù)列的前
是等比數(shù)列的前![]() 項的和,求
項的和,求![]()
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com