【題目】下列五個判斷：
①某校高二一班和高二二班的人數分別是m，n，某次測試數學平均分分別為a，b，則這兩個班的數學平均分為
；
②10名工人生產同一種零件，生產的件數分別是15，17，14，10，15，17，17，16，14，12，設其平均數為a，中位數為b，眾數為c，則有c>a>b；
③設m
,命題“若a>b，則
”的逆否命題為假命題；
④命題p“方程
表示橢圓”，命題q“
的取值范圍為1<<4”，則p是q的充要條件；
⑤線性相關系數r越大，兩個變量的線性相關性越強；反之，線性相關性越弱；
其中正確的個數有（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
①根據加權平均數的定義，計算即可；
②計算平均數、中位數、眾數即可；
③根據原命題和它的逆否命題真假性相同，判斷即可；
④命題p等價于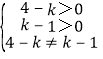
，即命題p：1<
<4且k
，結合q判斷即可；
⑤根據線性相關系數|r|越接近1，兩個變量的線性相關性越強，
|r|越接近0，兩個變量的線性相關性越弱判斷．
對于①，根據高二一班和高二二班的人數分別是m，n，平均分分別是a，b，
則這兩個班的平均分為
，∴①錯誤；
對于②，平均數為a
（15+17+14+10+15+17+17+16+14+12）＝14.7，
中位數為b＝15，眾數為c＝17，則有c＞b＞a，∴②錯誤；
對于③，m∈R，命題“若a＞b，則am2＞bm2”是假命題，
則它的逆否命題為假命題，③正確；
對于④，命題p等價于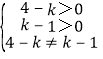，即命題p：1<<4且k；
又命題q“的取值范圍為1<<4”，所以 p是q的充分不必要條件，∴④錯誤；
對于⑤，線性相關系數|r|越接近1，兩個變量的線性相關性越強，
|r|越接近0，兩個變量的線性相關性越弱，∴⑤錯誤；
綜上，正確的命題為③，有1個．
故選：B．
優等生題庫系列答案科目：高中數學 來源： 題型：
【題目】2017年是某市大力推進居民生活垃圾分類的關鍵一年，有關部門為宣傳垃圾分類知識，面向該市市民進行了一次“垃圾分類知識”的網絡問卷調查，每位市民僅有一次參與機會，通過抽樣，得到參與問卷調查中的1000人的得分數據，其頻率分布直方圖如圖所示：
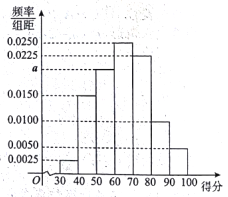
(Ⅰ)估計該組數據的中位數、眾數；
(Ⅱ)由頻率分布直方圖可以認為，此次問卷調查的得分Z服從正態分布N(μ，210)，μ近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表)，利用該正態分布，求P(50.5<Z<94)；
(Ⅲ)在(Ⅱ)的條件下，有關部門為此次參加問卷調査的市民制定如下獎勵方案：
(i)得分不低于μ可獲贈2次隨機話費，得分低于μ則只有1次；
(ii)每次贈送的隨機話費和對應概率如下：
贈送話費(單元：元) | 10 | 20 |
概率 |
|
|
現有一位市民要參加此次問卷調查，記X(單位：元)為該市民參加.問卷調查獲贈的話費，求X的分布列和數學期望.
附： 
，
若ZN(μ，σ2)，則P(μ－σ<Z<μ+σ)= 0.6826，P(μ－2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，已知兩點
， 
，動點
滿足
，線段
的中垂線交線段
于
點.
（1）求
點的軌跡
的方程；
（2）過點
的直線
與軌跡
相交于
兩點，設點
，直線
的斜率分別為
，問
是否為定值？并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】心理學家發現視覺和空間能力與性別有關，某數學興趣小組為了驗證這個結論，從興趣小組中按分層抽樣的方法抽取50名同學，給所有同學幾何和代數各一題，讓各位同學自由選擇一道題進行解答，統計情況如下表：（單位：人）
幾何題 | 代數題 | 總計 | |
男 同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
（1）能否據此判斷有97.5%的把握認為視覺和空間能力與性別有關？
（2）現從選擇幾何題的8名女生中任意抽取兩人對他們的答題進行研究，記甲、乙兩名女生被抽到的人數為
，求
的分布列及數學期望.
附表及公式：
| 0.15 | 0．10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
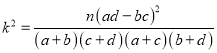
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
