
【題目】如圖所示,底面為菱形的直四棱柱![]() 被過三點(diǎn)
被過三點(diǎn)![]() 的平面截去一個(gè)三棱錐
的平面截去一個(gè)三棱錐![]() (圖一)得幾何體
(圖一)得幾何體![]() (圖二),E為
(圖二),E為![]() 的中點(diǎn).
的中點(diǎn).
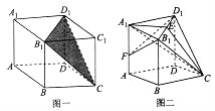
(1)點(diǎn)F為棱![]() 上的動(dòng)點(diǎn),試問平面
上的動(dòng)點(diǎn),試問平面![]() 與平面
與平面![]() 是否垂直?請(qǐng)說明理由;
是否垂直?請(qǐng)說明理由;
(2)設(shè)![]() ,當(dāng)點(diǎn)F為
,當(dāng)點(diǎn)F為![]() 中點(diǎn)時(shí),求銳二面角
中點(diǎn)時(shí),求銳二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)利用直四棱柱的幾何特征可知![]() ,
,![]() B1D1⊥平面CEA1,從而平面
B1D1⊥平面CEA1,從而平面![]() 平面CEA1 ;(2) 分別以
平面CEA1 ;(2) 分別以![]() 所在直線為
所在直線為![]() 軸的正方向,建立空間直角坐標(biāo)系,求出平面
軸的正方向,建立空間直角坐標(biāo)系,求出平面![]() 與平面F
與平面F![]() 的法向量,代入公式即可得到銳二面角
的法向量,代入公式即可得到銳二面角![]() 的余弦值.
的余弦值.
(1)平面![]() 平面
平面![]() ,證明如下:
,證明如下:
連接AC,BD相交于點(diǎn)O,
因?yàn)榈酌?/span>ABCD為菱形,所以AC⊥BD,
又因?yàn)橹彼睦庵舷碌酌嫒龋?/span>
所以由AC⊥BD得![]() ,
,
又因?yàn)?/span>CB=CD,![]() ,
,
所以CB1=CD1.
因?yàn)?/span>E為B1D1的中點(diǎn),所以![]() ,
,
又![]() ,所以B1D1⊥平面CEA1,
,所以B1D1⊥平面CEA1,
又因?yàn)?/span>![]() 平面
平面![]() ,
,
所以平面![]() 平面CEA1.
平面CEA1.
(2)連接OE,易知OE⊥平面ABCD,所以OB,OC,OE兩兩互相垂直,
所以分別以![]() 所在直線為
所在直線為![]() 軸的正方向,建立空間直角坐標(biāo)系,如圖所示,
軸的正方向,建立空間直角坐標(biāo)系,如圖所示,
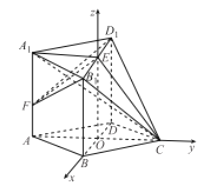
則O(0,0,0),![]() .(7分)
.(7分)
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則
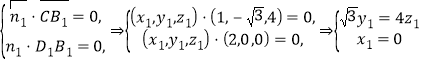 ,
,
令![]()
所以![]() .
.
同理設(shè)平面F![]() 的法向量為
的法向量為![]() ,則
,則
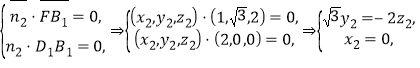 ,
,
令![]() .
.
所以![]() ,
,
所以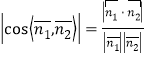
![]() ,
,
所以所求的銳二面角![]() 的余弦值為
的余弦值為![]()


 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百?gòu)?qiáng)名校期末沖刺100分系列答案
百?gòu)?qiáng)名校期末沖刺100分系列答案 好成績(jī)1加1期末沖刺100分系列答案
好成績(jī)1加1期末沖刺100分系列答案 金狀元績(jī)優(yōu)好卷系列答案
金狀元績(jī)優(yōu)好卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方體![]() 的棱長(zhǎng)為1,P,Q分別是線段
的棱長(zhǎng)為1,P,Q分別是線段![]() 和
和![]() 上的動(dòng)點(diǎn),且滿足
上的動(dòng)點(diǎn),且滿足![]() ,則下列命題錯(cuò)誤的是( )
,則下列命題錯(cuò)誤的是( )

A.存在P,Q的某一位置,使![]()
B.![]() 的面積為定值
的面積為定值
C.當(dāng)![]() 時(shí),直線
時(shí),直線![]() 與
與![]() 是異面直線
是異面直線
D.無論P,Q運(yùn)動(dòng)到任何位置,均有![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國(guó)古代著名的數(shù)學(xué)家劉徽著有《海島算經(jīng)》.內(nèi)有一篇:“今有望海島,立兩表齊、高三丈,前后相去千步,今后表與前表相直,從前表卻行百二十三步,人目著地望島峰,與表末參合.從后表卻行百二十七步,人目著地取望島峰,亦與表末參合.問島高及去表各幾何?”(參考譯文:假設(shè)測(cè)量海島,立兩根標(biāo)桿,高均為5步,前后相距1000步,令前后兩根標(biāo)桿的底部和島的底部在同一水平直線上,從前標(biāo)桿退行123步,人的視線從地面(人的高度忽略不計(jì))過標(biāo)桿頂恰好觀測(cè)到島峰,從后標(biāo)桿退行127步,人的視線從地面過標(biāo)桿頂恰好觀測(cè)到島峰,問島高多少?島與前標(biāo)桿相距多遠(yuǎn)?)(丈、步為古時(shí)計(jì)量單位,三丈=5步).則海島高度為
A. 1055步 B. 1255步 C. 1550步 D. 2255步
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,且
,且![]() (
(![]() ).
).
(1)求![]() ;
;
(2)設(shè)函數(shù) ,
,![]() (
(![]() ),求數(shù)列
),求數(shù)列![]() 的前n項(xiàng)和
的前n項(xiàng)和![]() ;
;
(3)設(shè)![]() 為實(shí)數(shù),對(duì)滿足
為實(shí)數(shù),對(duì)滿足![]() 且
且![]() 的任意正整數(shù)m,n,k,不等式
的任意正整數(shù)m,n,k,不等式![]()
![]() 恒成立,試求實(shí)數(shù)
恒成立,試求實(shí)數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)關(guān)于某種設(shè)備的使用年限![]() (年)與所支出的維修費(fèi)用
(年)與所支出的維修費(fèi)用![]() (萬元)有如下統(tǒng)計(jì):
(萬元)有如下統(tǒng)計(jì):
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 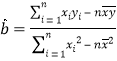 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 與
與![]() 具有線性相關(guān)關(guān)系,求出線性回歸方程;
具有線性相關(guān)關(guān)系,求出線性回歸方程;
(3)估計(jì)使用年限為10年時(shí),維修費(fèi)用約是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系中,直線l的參數(shù)方程為![]() (t為參數(shù),
(t為參數(shù),![]() ),以坐標(biāo)原點(diǎn)為極點(diǎn),
),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為
軸正半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]() .
.
(1)當(dāng)![]() 時(shí),寫出直線l的普通方程及曲線C的直角坐標(biāo)方程;
時(shí),寫出直線l的普通方程及曲線C的直角坐標(biāo)方程;
(2)已知點(diǎn)![]() ,設(shè)直線l與曲線C交于A,B兩點(diǎn),試確定
,設(shè)直線l與曲線C交于A,B兩點(diǎn),試確定![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在定義域上是單調(diào)增函數(shù),求實(shí)數(shù)a的取值范圍;
在定義域上是單調(diào)增函數(shù),求實(shí)數(shù)a的取值范圍;
(2)討論![]() 的極值點(diǎn)的個(gè)數(shù);
的極值點(diǎn)的個(gè)數(shù);
(3)若![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的前n項(xiàng)和為Sn,a1=3,an+1=2Sn+3(n∈N*).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)bn=log3an,若數(shù)列![]() 的前n項(xiàng)和為Tn,證明:Tn<1.
的前n項(xiàng)和為Tn,證明:Tn<1.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com