【題目】在銳角△ABC中，內(nèi)角A，B，C的對邊分別為a，b，c，且2asinB= 
b．
（1）求角A的大小；
（2）若a=6，b+c=8，求△ABC的面積．
【答案】
（1）解：由2asinB= 
b，利用正弦定理得：2sinAsinB= sinB，
∵sinB≠0，∴sinA= 
，
又A為銳角，
則A= 
；
（2）解：由余弦定理得：a2=b2+c2﹣2bccosA，即36=b2+c2﹣bc=（b+c）2﹣3bc=64﹣3bc，
∴bc= 
，又sinA= ，
則S△ABC= 
bcsinA= 
【解析】（1）利用正弦定理化簡已知等式，求出sinA的值，由A為銳角，利用特殊角的三角函數(shù)值即可求出A的度數(shù)；（2）由余弦定理列出關(guān)系式，再利用完全平方公式變形，將a，b+c及cosA的值代入求出bc的值，再由sinA的值，利用三角形面積公式即可求出三角形ABC的面積．
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
．
（I）當
時，求
的單調(diào)區(qū)間和極值；
（II）若對于任意
，都有
成立，求k的取值范圍；
(Ⅲ)若
，且
，證明：
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)函數(shù)
.
(Ⅰ)當
時，求函數(shù)
的單調(diào)區(qū)間；
(Ⅱ)若函數(shù)
有兩個極值點
，且
，求證: 
；
(Ⅲ)設(shè)
，對于任意
，總存在
，使
成立，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
分別是橢圓
的長軸與短軸的一個端點， 
是橢圓的左、右焦點，以
點為圓心、3為半徑的圓與以
點為圓心、1為半徑的圓的交點在橢圓
上，且
．
（1）求橢圓
的方程；
（2）設(shè)
為橢圓
上一點，直線
與
軸交于點
，直線
與
軸交于點
，求證： 
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）= 
，把函數(shù)g（x）=f（x）﹣x的零點按從小到大的順序排列成一個數(shù)列，則該數(shù)列的通項公式為（ ）
A.
B.an=n﹣1
C.an=n（n﹣1）
D.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】甲乙兩個學校高三年級分別有1100人，1000人，為了了解兩個學校全體高三年級學生在該地區(qū)二模考試的數(shù)學成績清況，采用分層抽樣方法從兩個學校一共抽取了105名學生的數(shù)學成績，并作出了頻數(shù)分布統(tǒng)計表如下：
甲校：
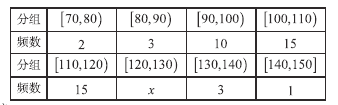
乙校:
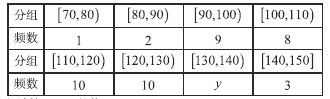
（1）計算
的值；
（2）若規(guī)定考試成績在
內(nèi)為優(yōu)秀，請根據(jù)樣本估計乙校數(shù)學成績的優(yōu)秀率；
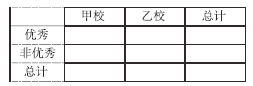
（3）由以上統(tǒng)計數(shù)據(jù)填寫下面
列聯(lián)表，并判斷是否有
的把握認為兩個學校的數(shù)學成績有差異.
附：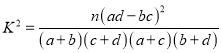 
； 
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在△ABC中，內(nèi)角A，B，C的對邊分別為a，b，c，2cos（A﹣C）+cos2B=1+2cosAcosC．
（1）求證：a，b，c依次成等比數(shù)列；
（2）若b=2，求u=| 
|的最小值，并求u達到最小值時cosB的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知向量 
=（cos 
x，sin x）， 
=（cos 
，﹣sin ），且x∈[﹣ 
， 
]
（1）求 及| + |；
（2）若f（x）= ﹣| + |，求f（x）的最大值和最小值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
