
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若對(duì)于任意![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ) ![]() ;(Ⅱ)單調(diào)遞增區(qū)間是
;(Ⅱ)單調(diào)遞增區(qū)間是![]() ;
; ![]() 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是![]() ;(Ⅲ)答案見(jiàn)解析.
;(Ⅲ)答案見(jiàn)解析.
【解析】試題分析:(Ⅰ)由f(1)=0,f′(1)=1;從而寫(xiě)出切線方程即可;
(Ⅱ)根據(jù)導(dǎo)數(shù),求出導(dǎo)數(shù)等于0的根,分析導(dǎo)數(shù)函數(shù)值在根的左右的正負(fù)變化即可得出![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)當(dāng)![]() 時(shí),“
時(shí),“![]() ”等價(jià)于“
”等價(jià)于“![]() ”.令
”.令![]() ,
, ![]() ,求導(dǎo)研究單調(diào)性求出
,求導(dǎo)研究單調(diào)性求出![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ,即可求出實(shí)數(shù)
,即可求出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
試題解析:
(Ⅰ)因?yàn)楹瘮?shù)![]() ,
,
所以![]() ,
,
![]() .
.
又因?yàn)?/span>![]() ,
,
所以曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅱ)函數(shù)![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,
,
由(Ⅰ)可知, ![]() .
.
令![]() 解得
解得![]() .
.
![]() 與
與![]() 在區(qū)間
在區(qū)間![]() 上的情況如下:
上的情況如下:
x |
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ |
所以, ![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ;
;
![]() 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是![]() .
.
(Ⅲ)當(dāng)![]() 時(shí),“
時(shí),“![]() ”等價(jià)于“
”等價(jià)于“![]() ”.
”.
令![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞減.
單調(diào)遞減.
當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增.
單調(diào)遞增.
而![]() ,
, ![]()
所以![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() .
.
所以當(dāng)![]() 時(shí),對(duì)于任意
時(shí),對(duì)于任意![]() ,都有
,都有![]() .
.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)函數(shù)f(x)=xsinx,現(xiàn)有下列命題:①函數(shù)f(x)是偶函數(shù);②函數(shù)f(x)的最小正周期是2π;③點(diǎn)(π,0)是函數(shù)f(x)的圖象的一個(gè)對(duì)稱(chēng)中心;④函數(shù)f(x)在區(qū)間![]() 上單調(diào)遞增,在區(qū)間
上單調(diào)遞增,在區(qū)間![]() 上單調(diào)遞減.其中是真命題的是________.(寫(xiě)出所有真命題的序號(hào))
上單調(diào)遞減.其中是真命題的是________.(寫(xiě)出所有真命題的序號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了迎接第二屆國(guó)際互聯(lián)網(wǎng)大會(huì),組委會(huì)對(duì)報(bào)名參加服務(wù)的![]() 名志愿者進(jìn)行互聯(lián)網(wǎng)知識(shí)測(cè)試,從這
名志愿者進(jìn)行互聯(lián)網(wǎng)知識(shí)測(cè)試,從這![]() 名志愿者中采用隨機(jī)抽樣的方法抽取
名志愿者中采用隨機(jī)抽樣的方法抽取![]() 人,所得成績(jī)?nèi)缦拢?/span>
人,所得成績(jī)?nèi)缦拢?/span> ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)作出抽取的![]() 人的測(cè)試成績(jī)的莖葉圖,以頻率為概率,估計(jì)這
人的測(cè)試成績(jī)的莖葉圖,以頻率為概率,估計(jì)這![]() 志愿者中成績(jī)不低于
志愿者中成績(jī)不低于![]() 分的人數(shù);
分的人數(shù);
(2)從抽取的成績(jī)不低于![]() 分的志愿者中,隨機(jī)選
分的志愿者中,隨機(jī)選![]() 名參加某項(xiàng)活動(dòng),求選取的
名參加某項(xiàng)活動(dòng),求選取的![]() 人恰有一人成績(jī)不低于
人恰有一人成績(jī)不低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知線段AB的端點(diǎn)B的坐標(biāo)為(3,0),端點(diǎn)A在圓![]() 上運(yùn)動(dòng);
上運(yùn)動(dòng);
(1)求線段AB中點(diǎn)M的軌跡方程;
(2)過(guò)點(diǎn)C(1,1)的直線m與M的軌跡交于G、H兩點(diǎn),當(dāng)△GOH(O為坐標(biāo)原點(diǎn))的面積最大時(shí),求直線m的方程并求出△GOH面積的最大值.
(3)若點(diǎn)C(1,1),且P在M軌跡上運(yùn)動(dòng),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】過(guò)點(diǎn)![]() 的直線
的直線![]() 與
與![]() 軸正半軸和
軸正半軸和![]() 軸正半軸分別交于
軸正半軸分別交于![]() ,
,![]()
(1)當(dāng)![]() 為
為![]() 的中點(diǎn)時(shí),求
的中點(diǎn)時(shí),求![]() 的方程
的方程
(2)當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的方程
的方程
(3)當(dāng)![]() 面積取到最小值時(shí),求
面積取到最小值時(shí),求![]() 的方程
的方程
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了讓貧困地區(qū)的孩子們過(guò)一個(gè)溫暖的冬天,某校陽(yáng)光志愿者社團(tuán)組織“這個(gè)冬天不再冷”冬衣募捐活動(dòng),共有50名志愿者參與.志愿者的工作內(nèi)容有兩項(xiàng):①到各班做宣傳,倡議同學(xué)們積極捐獻(xiàn)冬衣;②整理、打包募捐上來(lái)的衣物.每位志愿者根據(jù)自身實(shí)際情況,只參與其中的某一項(xiàng)工作.相關(guān)統(tǒng)計(jì)數(shù)據(jù)如下表所示:

(1)如果用分層抽樣的方法從參與兩項(xiàng)工作的志愿者中抽取5人,再?gòu)倪@5人中選2人,那么“至少有1人是參與班級(jí)宣傳的志愿者”的概率是多少?
(2)若參與班級(jí)宣傳的志愿者中有12名男生,8名女生,從中選出2名志愿者,用![]() 表示所選志愿者中的女生人數(shù),寫(xiě)出隨機(jī)變量
表示所選志愿者中的女生人數(shù),寫(xiě)出隨機(jī)變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某圖書(shū)公司有一款圖書(shū)的歷史收益率(收益率=利潤(rùn)÷每本收入)的頻率分布直方圖如圖所示:
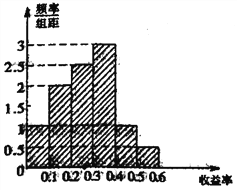
(1)試估計(jì)平均收益率;(用區(qū)間中點(diǎn)值代替每一組的數(shù)值)
(2)根據(jù)經(jīng)驗(yàn),若每本圖書(shū)的收入在20元的基礎(chǔ)上每增加![]() 元,對(duì)應(yīng)的銷(xiāo)量
元,對(duì)應(yīng)的銷(xiāo)量![]() (萬(wàn)份)與
(萬(wàn)份)與![]() (元)有較強(qiáng)線性相關(guān)關(guān)系,從歷史銷(xiāo)售記錄中抽樣得到如下5組
(元)有較強(qiáng)線性相關(guān)關(guān)系,從歷史銷(xiāo)售記錄中抽樣得到如下5組![]() 與
與![]() 的對(duì)應(yīng)數(shù)據(jù):
的對(duì)應(yīng)數(shù)據(jù):

據(jù)此計(jì)算出的回歸方程為![]()
①求參數(shù)![]() 的估計(jì)值;
的估計(jì)值;
②若把回歸方程![]() 當(dāng)作
當(dāng)作![]() 與
與![]() 的線性關(guān)系,
的線性關(guān)系, ![]() 取何值時(shí),此產(chǎn)品獲得最大收益,并求出該最大收益.
取何值時(shí),此產(chǎn)品獲得最大收益,并求出該最大收益.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)該三棱錐的截面EFGH平行于AB、CD,分別交AD、AC、BC、BD于E、F、G、H.

(1)證明:AB⊥CD;
(2)求截面四邊形EFGH面積的最大值,并說(shuō)明面積取最大值時(shí)截面的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() ,拋物線
,拋物線![]() :
:![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,射線
,射線![]() 與拋物線
與拋物線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,與其準(zhǔn)線相交于點(diǎn)
,與其準(zhǔn)線相交于點(diǎn)![]() ,則
,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com